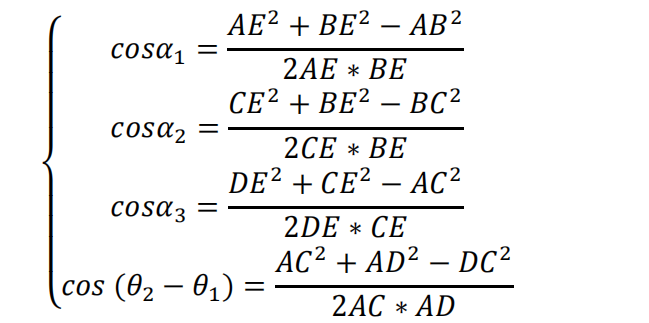PART.01原题重现
PART.02评阅要点
本题涉及无人机集群协同编队控制问题，讨论无人机集群在保持编队飞行时，如何通过部分无人机发射信号、其余无人机被动接收信号，利用提取的方向信息进行定位，进而调整无人机的位置。
问题1
(1)在本问中，位于圆心的无人机和圆周上2架编号已知且位置无偏差的无人机发射信号，需建立其他接收信号、位置略有偏差的无人机的定位模型。鼓励给出定位模型的解析解。
注 只能利用接收的方向角度信息，不能利用未知的距离信息。最终应给出当前无人机的位置信息。
(2)本问中接收信号无人机的位置略有偏差，发射信号的无人机位置无偏差，但除2架(其中1架位于中心)无人机外，其他发射信号的无人机编号未知。应明确给出还需要几架无人机发射信号才能实现有效定位，及相应的定位方案。
注能明确给出编号未知的发射信号无人机最小架数为1的结论为佳。
(3)本问中发射信号和接收信号的无人机位置均略有偏差，调整策略为每次选择位于中心及圆周上最多3架无人机来发射信号，通过多次调整，最终实现9架无人机均匀分布在某个圆周上的目标。
注：
①发射信号的无人机位置也有偏差;
②题目中并没有给出无人机彼此之间可以进行通信的条件。将不同无人机获取的方向角度信息进行共享，不完全符合题意;
③假设发射信号的无人机可以同时接收信号，不完全符合题意;
④在利用题目中所给出的数据进行验证时，只能依据方向角度信息进行调整，不能直接利用坐标信息，坐标信息仅用于生成方向角度信息;
⑤给出只需要圆周上2架无人机来遂行发射信号的有效调整方案更好;
⑥应明确给出调整的终止条件及调整结果的评价标准;
⑦调整方案及数值验证给出的调整结果不唯一，与所采用的策略有关。
问题2
本问可以考虑不同的编队队形，相应的调整方案亦不唯一。例如针对锥形队形，可以借鉴问题1中对具有圆周均匀分布队形的调整策略，采用形成六等分圆的方式进行逐步调整，也可采用分层的调整方案，大雁领队方式或其他合理的策略。应给出不同的初值进行仿真实验，并给出调整的终止条件及调整结果的评价标准。
PART.03问题精简
问题一
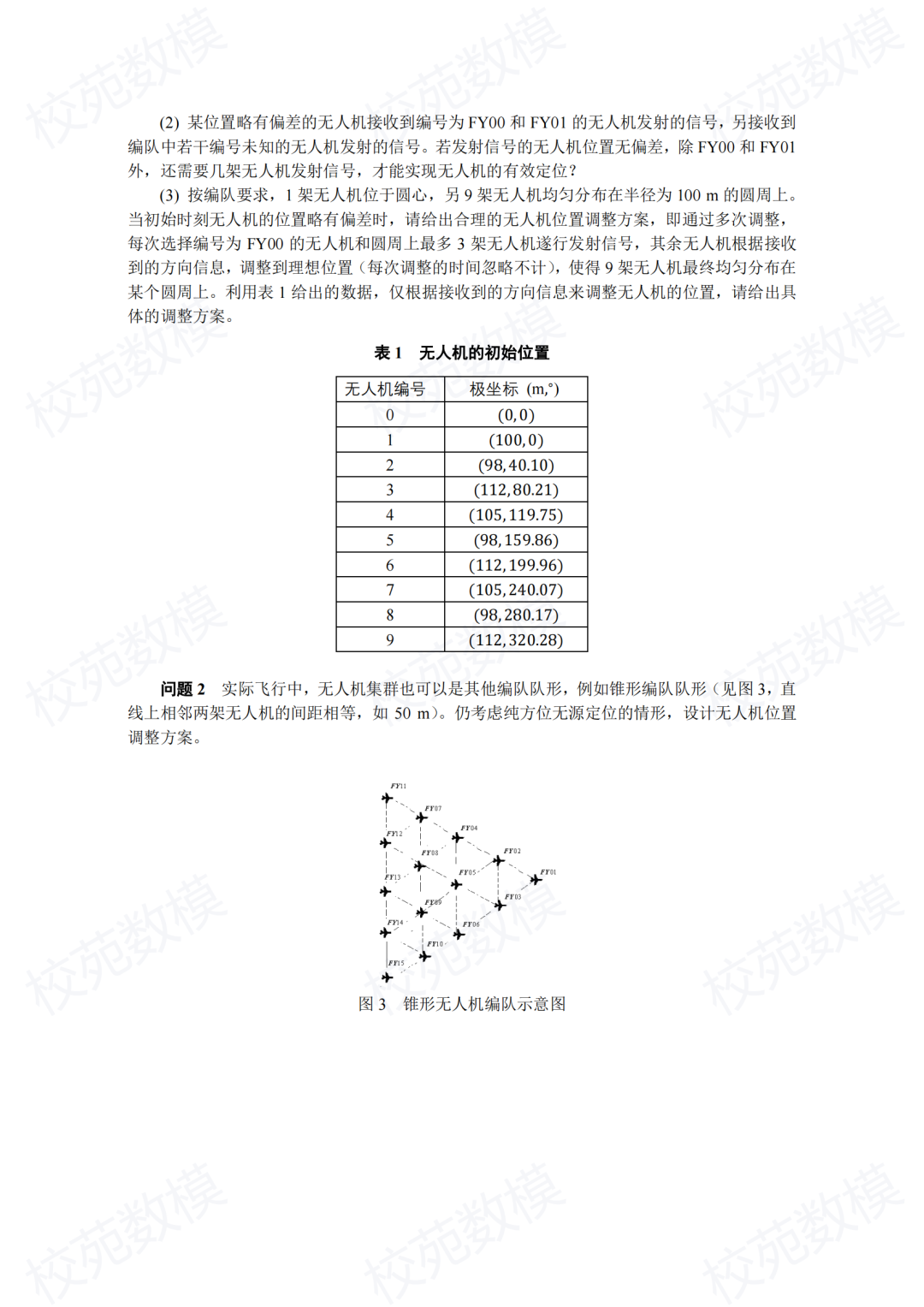
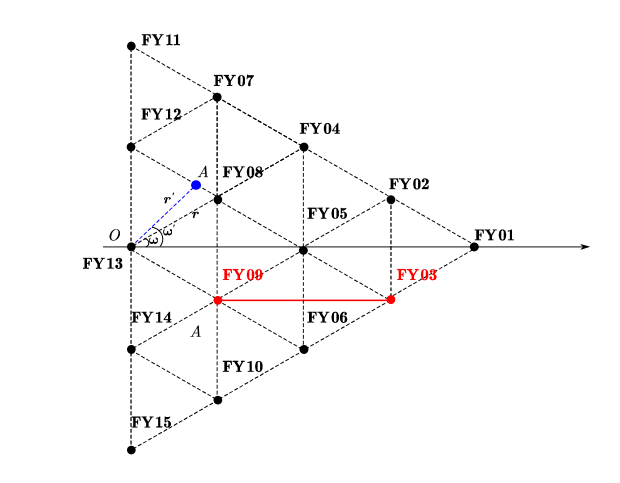
问题一的第一问，主要是对由 10 架无人机形成的圆形编队进行研究。其中，9 架无人机（FY01~FY09）平均分布在圆周上，另外一架无人机（FY00）则位于圆心。FY00 与编队中另外两架编号明确且位置精确的无人机发出信号，而其他位置稍有误差的无人机则接收这些信号。需要建立一个用于接收信号的无人机的定位模型。
问题一的第二问，是在第一问的无人机定位模型基础上，考虑这样的情况：编号为 FY00、FY01 以及若干架位置精确的无人机发出信号，其他的无人机则接收这些信号。需要求解的是，除了 FY00 和 FY01 之外，最少需要多少架发出信号的无人机，才能实现无人机的有效定位。
问题一的第三问，是根据无人机的初始位置信息，设计出具体的调整策略。每次可以选择 FY00 以及最多 3 架圆周上的无人机发出信号，目标是让 9 架无人机最终能够均匀分布在某个半径为 100 m 的圆周上。
问题二
思考无人机锥形编队形态，如题中所示，相邻无人机之间的直线距离相等，研究纯方位无源定位下无人机位置的调整策略。
PART.04问题分析问题一
第一问针对问题一的第一问，需要构建一个定位模型，其中发射信号的无人机编号明确且位置精确。这个问题主要针对一个由 10 架无人机组成的圆形编队，9 架无人机（FY01~FY09）均匀分布在圆周上，另一架无人机（FY00）位于圆心。FY00 和编队中另外两架编号明确且位置精确的无人机发出信号，其他位置略有误差的无人机则接收这些信号。 为了解决这个问题，首先需要将无人机略微偏差的飞行位置限制在合理范围内。这里给出如下范围限制：
由于不同发射信号的无人机与接收信号的无人机的相对位置存在差异，因此将其按照相对位置关系划分为两类。相对位置划分如下：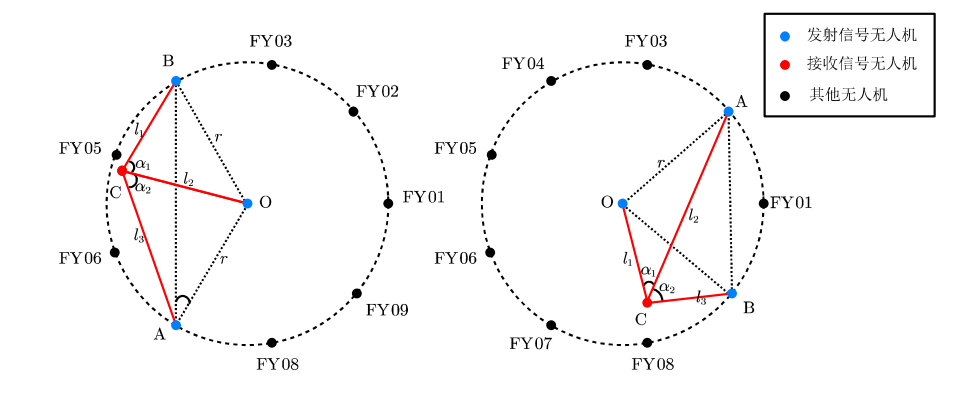
鉴于无人机 FY01~FY09 均匀分布在某一圆周上，可以根据无人机接收到的方向信息等列出方程，建立基于方向信息的二维定位模型。最后，通过随机模拟符合位置范围限制的数据点进行模型验证。
第二问
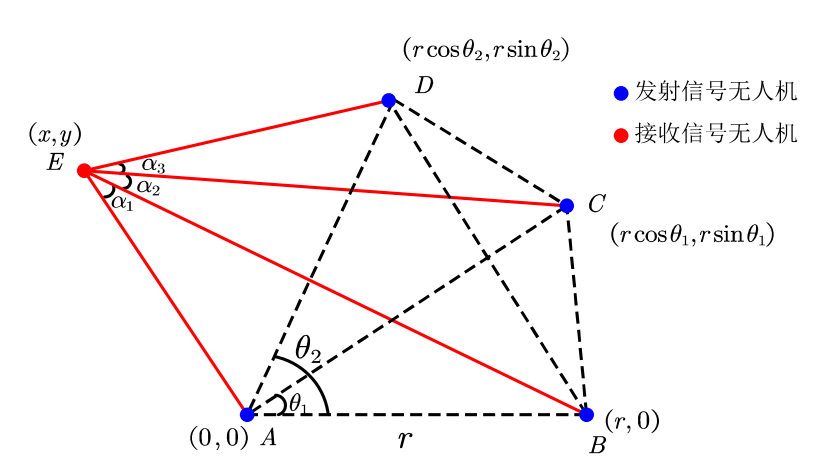
对于问题一的第二问，我们需要构建一个有效的定位模型，在这种模型中，发射信号的无人机编号信息是未知的。在第一问中，我们发现引入一架编号信息未知的无人机无法实现有效定位。因此，在第一问模型的基础上，除了 FY00 和 FY01，我们还需要两架无人机发射信号，以建立一个四点定位模型。如下图所示：
利用余弦定理得到四点定位模型：
最后，为了评估模型的精度，我们一方面查阅文献，引入定位精度的量化衡量指标——几何精度因子（GDOP）；另一方面，我们使用实际数据来测试这个模型。
第三问
在问题一的前两问，我们都在假设发射信号的无人机位置是精确无误的。然而，如果发射信号的无人机位置存在误差，那么这种定位模型就不能再适用了。对于问题一的第三问，需要根据初始的极坐标数据，给出具体的无人机调整策略。根据四点定位模型，我们需要两架位置编号已知的无人机和两架位置编号未知的无人机对其他无人机进行定位。
首先，选择位置无偏差的无人机 FY00 和 FY01 发射信号，并再引入两架无人机发射信号，根据偏差角度的最小值来选择这两架无人机。
然后，为了给出无人机的调整策略，可以构建一个单目标优化模型，并采用分轮迭代的调整策略。以无人机的位置作为决策变量，以各个无人机与其正确位置的偏差程度的平方和最小化为目标函数，并以无人机偏差程度的逐轮降低、位置更新条件的阈值、调整花费成本最小等作为约束条件。在每一轮调整中，选择四架发射信号的无人机，对其他六架接收信号的无人机进行位置调整。经过迭代调整后，使各个无人机大致均匀分布在半径为 100m 的圆周上。
问题二
在问题二中，针对锥形编队队形，利用纯方位无源定位法设计一种位置调整方案。按照问题一的建模思路，首先考虑发射信号无人机编号已知且位置准确的情况，然后考虑发射信号的无人机编号未知且位置准确的情况。对于这两种情况，可以通过数学推导轻松地获得定位调整方案。
然而，当发射信号无人机位置存在偏差时，情况变得复杂，需要采用迭代计算的方法进行调整。 类似于问题一的第三问，首先根据选取规则（即假设初始两架无人机的位置不存在偏差，且连线上不存在其他无人机）指定位置无偏差的无人机 FY03 和 FY09 发射信号，然后随机给出锥形无人机编队初始极坐标数据。
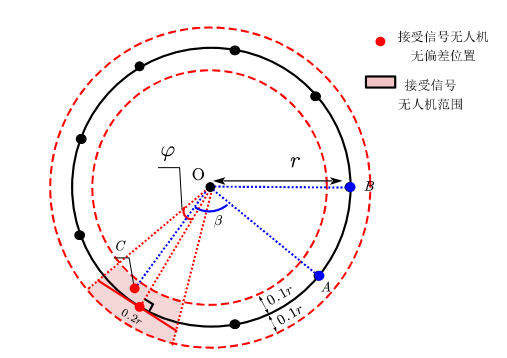
在此基础上，需要再引入两架无人机发射信号，根据偏差角度绝对值最小的原则来选择这两架无人机。偏差角度和偏差距离示意图如下：
接下来，为了给出无人机的调整方案，构建一个单目标优化模型，并采用分轮迭代的调整策略。以无人机的位置作为决策变量，以各个无人机与其正确位置的偏差程度的平方和最小化为目标函数，并以无人机偏差程度的逐轮降低、位置更新条件的阈值、调整花费成本最小等作为约束条件。在每一轮调整中，选择四架发射信号的无人机，对其余接收信号的无人机同时进行位置调整。经过迭代调整后，使各个无人机大致分布在其准确位置上。
PART.05模型假设
01假设:被动接收的信号无人机同时接收不同发射信号，即不考虑存在的时间差。 原因：仅考虑利用接收的方位角进行无人机定位，忽略时差、距离等因素干扰。
02假设:接收信号无人机位置不会出现较大偏差，飞行偏差在合理范围内。 原因：本文仅飞行位置略有偏差的无人机进行定位和调整，忽略飞行位置偏差过大（超过偏差阈值）的无人机。
03假设:在选取发射信号的无人机时优先考虑位置精确的无人机。 原因：定位模型中的定位误差在一定程度上受到发射点位置误差的影响。
PART.06优秀论文摘要欣赏
【竞赛报名/项目咨询+微信：mollywei007】
