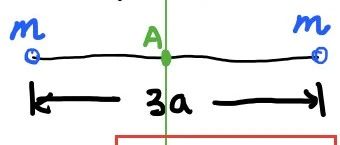
之前介绍了杨氏模量 (Young's modulus) 的概念,这次我们来做一下关于杨氏模量的 BPhO 竞赛题,这是 Section2 的其中一问,难度比较大。不看答案,自己能不能做出来?
A piece of elastic cord of length  and cross-sectional area A is stretched to twice its natural length. Assuming that the total volume remains constant, and that cross-sectional area is uniform along its length, and the Young's modulus E for the material remains constant,
and cross-sectional area A is stretched to twice its natural length. Assuming that the total volume remains constant, and that cross-sectional area is uniform along its length, and the Young's modulus E for the material remains constant,
(i) obtain an expression for the final tension in terms of E and A.
(ii) Show that the work done in stretching the elastic is given by:

答案解析:
(i) 题目中说把弹力绳 (elastic cord) 抻长为原长的 2 倍,同时体积不能变,横截面积保持一致,先做个图:

上图为弹性绳在力的作用下被抻长为原长的 2 倍,此过程体积不变,所以:
 被抻长后,弹性绳的横截面积 A' 变为原来的二分之一。
被抻长后,弹性绳的横截面积 A' 变为原来的二分之一。
目前弹性绳形变情况已知,要求受力情况,把形变和受力联结起来的物理量是杨氏模量,所以根据定义展开杨氏模量:
 当弹性绳被抻长到
当弹性绳被抻长到  时,上式中的 F 即是我们要求的 final tension,此时弹性绳的横截面积是 A' = A / 2,伸长量
时,上式中的 F 即是我们要求的 final tension,此时弹性绳的横截面积是 A' = A / 2,伸长量  ,原长还是
,原长还是  ,代入上式有:
,代入上式有:

即为本题答案。
(ii) 小问中需求拉伸弹性绳的过程中外力所做的功。弹性绳越长、弹力越大,又因为外力等于弹力,所以外力 F 也是一个逐渐增大的变力。如果力是定值,且和位移在同一方向上,那么做功公式是:W = F s;本题中是变力做功,需要用到积分公式,即:
 为了展开积分公式中的 F,我们接下来要找到力 F 与向右的位移 x 的关系,作图更加直观:
为了展开积分公式中的 F,我们接下来要找到力 F 与向右的位移 x 的关系,作图更加直观:
 由于都是将弹性绳拉长
由于都是将弹性绳拉长 ,两个力在两端拉、和只有一端的力拉所做的功是一样的。为了简化问题,我们索性把弹性绳左端固定在墙壁上,只研究弹性绳右侧力 F(x) 将弹性绳拉伸
,两个力在两端拉、和只有一端的力拉所做的功是一样的。为了简化问题,我们索性把弹性绳左端固定在墙壁上,只研究弹性绳右侧力 F(x) 将弹性绳拉伸  所做的功。如上图,以弹性绳右端点为原点,向右作 x 轴,以此来研究力 F(x) 随位移 x 的变化。
所做的功。如上图,以弹性绳右端点为原点,向右作 x 轴,以此来研究力 F(x) 随位移 x 的变化。
假设力 F(x) 将弹性绳抻长任意距离 x,如下图绿线所示:

此时,弹性绳长度变为  ,但整个过程中体积不变,所以新的横截面积 A’ 就是:
,但整个过程中体积不变,所以新的横截面积 A’ 就是:

横截面积有了,我们还是像上一个小问一样,把杨氏模量按其定义展开:

当弹性绳伸长 x 以后,上式中的长度变化  即为 x,横截面积 A 为 A',代入上式有:
即为 x,横截面积 A 为 A',代入上式有:

由此找到了力 F 随形变量 x 变化的通式。不妨验证一下:将  代入上式,得出的 F 与第 1 小问结果相符,具有一致性。
代入上式,得出的 F 与第 1 小问结果相符,具有一致性。
下面将 F(x) 代入变力做功的积分公式,进行数学计算后即为本题答案。注意积分的下限是弹性绳起始状态、不受力,有  ;积分上限对应末状态,即
;积分上限对应末状态,即  :
: