注：由于部分字符无法加载导致题目不完成，完整题目截图已经放在文章最后，请自行查看。
- Niek有块正方形卡片，每块的一面为黄色，另一面为红色．他将卡片摆成一个的大正方形，其中一些卡片黄色一面朝上，一些卡片红色一面朝上．对于每种摆放方式，如下计算其“单色性”．对每一对有公共边的卡片，按如下规则分别记为或：如果两块有公共边的卡片颜色相同，则记为；如果两块有公共边的卡片颜色不同，则记为．然后将所有得到的数全部相加（结果可能为负）．例如，如果将卡片如下图摆放，则存在对有公共边的卡片颜色相同，存在对有公共边的卡片颜色不同．
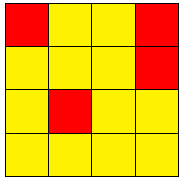因此，上图的“单色性”为：．Niek考察了所有卡片的摆放方法，并列出所有能取得的“单色性”的值．
(a)求出Niek列出的数中最大的三个数，并说明理由．
(b)求出Niek列出的数中最小的三个数，并说明理由．
(c)求出Niek列出的数中最小的正数，并说明理由． - 有()支队伍参加一次比赛，其中每两支队伍至多进行一场比赛．如果任意四支参赛队伍之间恰好进行了三场比赛，则称这次比赛是“平衡的”．求的最大值，使得存在支队伍参加的“平衡的”比赛．
- 一只青蛙在平面上的网格点上跳来跳去，每次从一个网格点跳到另一个网格点．青蛙从点出发，依次进行如下跳跃：水平方向跳跃个单位长度，竖直方向跳跃个单位长度，水平方向跳跃个单位长度，竖直方向跳跃个单位长度求所有的正整数，使得青蛙能在次跳跃后回到点．
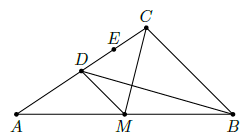
- 在中，．点为的中点，过作的平行线交于点．的中点为点，．求证：
(a)和相似．
(b)．
- 正整数满足：对的任意正约数，都有．求证：为素数．
【竞赛报名/项目咨询请加微信：mollywei007】
