新加坡数学教材详细介绍

在这个大摇号时代，随着国家减负力度越来越大，我们终于可以不用着急在学前抢跑了。

但减负不代表不用努力学习，而是要更明智，更长远的学习。所谓流水不争先，争的是滔滔不绝。

希望这篇文章能在数学学习方面，引发你进一步的思考，比如：学习数学的方式方法有哪些？如何更加科学合理地规划学习路线？如何培养数学思维？孩子积累的思维厚度能支撑他走多远？

我们在以前的文章说过，英语的学习规划，一定是越早越好。因为孩子年龄越小，语言天赋越高，学习效果越事半功倍。而对于数学思维的培养，则还需要稳扎稳打，将基础夯实。

纵观全球，亚洲学生数学好几乎是世界公认，而新加坡孩子的数学成绩又连续多年位居亚洲排名首位。

最新的国际数学与科学趋势研究报告（Trends in International Mathematics and Science Study，简称TIMSS）2019出炉——在四年一届的TIMSS（聚集全世界60多万年龄在9-14岁的学生参加的一项考察数学和科学的考试）考试中，新加坡中小学生的数理能力领先全球72个国家和地区的学生排名第一。

并且，新加坡是唯一有超过一半的小四生（54％）和中二生（51％）在数学方面取得优等的国家。而国际中位数分别是小四7％和中二5％。科学方面，新加坡38％的小四生和48％的中二生取得优等，国际中位数分别为小四6％和中二7％。

在全球前五名教育体系中，新加坡的“数理优等生”比率最高，35％的小四学生和42％的中二学生同时在数学和科学取得优等的最高等级，超越香港、韩国、日本等国家和地区。

而同年的PISA（聚集全世界72个国家54万15岁的学生进行的包括阅读、数学以及协作解决问题的能力测试）中，新加坡的学生也是总分排名第一，而更厉害的是，这些学生未经过培训，只是随机挑选出来的。

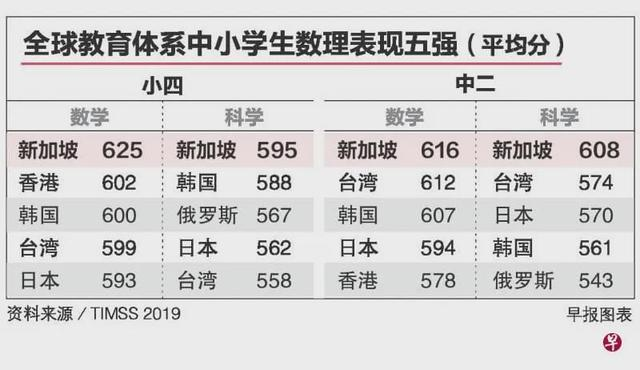
图源：联合早报

从以上的成绩我们可以看出，新加坡孩子整体的数学水平都很高。这是因为，新加坡的数学教育采取核心CPA教学法，这种教学法正符合孩子培养数学思维的路径。

CPA教学法，由美国教学心理专家、认知心理学家Jerome Bruner在60年代最先提出。他经观察发现，小孩子的学习，往往会经历三个阶段，分别是：

C-Concrete 具象化

P-Pictorial形象化

A- Abstract 抽象化

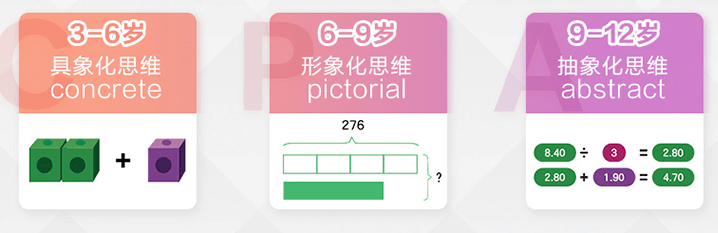
新加坡教辅SAP的王牌——“ 新加坡数学”正是遵循这种学习规律，通过建模找到生活和数学之间的连接点。

“新加坡数学”系列教材包括基础版'Learning Maths'，奥数版'SAP Maths Olympiad'、应用题练习册'101 Challengling Maths'， 从学龄前到小学6年级，全部覆盖。

比如“新加坡数学”的基础版'Learning Maths'利用图形帮助孩子从具象思维向抽象思维过渡，提升孩子的计算、应用、逻辑推理、空间想象、分类统计、归纳等多种数学能力，建立系统性数学思维，从而在解题时能快速理清解题思路，找到解决办法，培养了孩子系统的数学思维能力。

优点：

1.  启蒙版本注重知识点反复多方面诠释，让学生能全面认识。

2.  基础和提高版本注重数学建模，注重解决问题，modeling和problem solve都是学数学很关键的能力。

3.  这套书是应用建模modeling来解决问题的，解题思路和方式都很经典。 题目都是图形化和数字结合，这就是所谓的modeling的基础思想，孩子很容易理解这样的方式，数学就会越学越好。

4. 难度循序渐进，逐级上升。从幼儿园阶段认识10以内的数开始，循序渐近，逐步到一年级学习10、20、40、100以内的加减法、二年级简单的乘除法、货币、长度、重量、时间的换算，以及三年级几何点、线、面、角的概念，四年级分数、小数的基本认识，统计表的初步知识等等。

举个例子：

这是二年级乘法的学习过程。首先，用实物来作为学习乘法的入门，将乘法具象化。

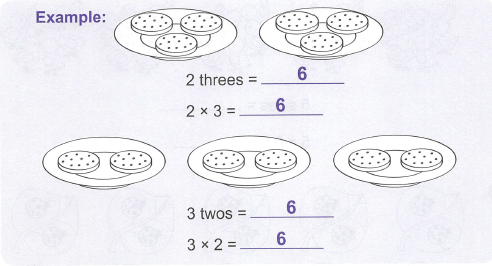
接下来，让学生进行这方面的练习。

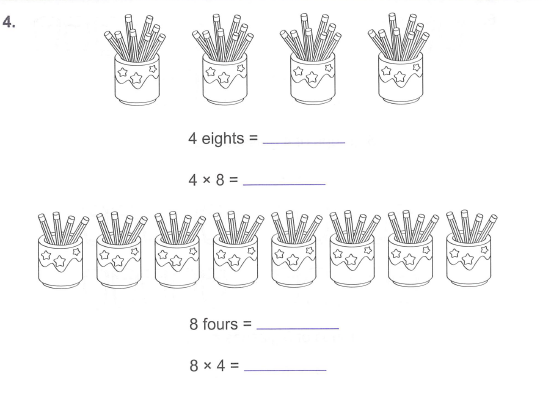
再通过具象，更加直观地理解乘法与加法的关系。

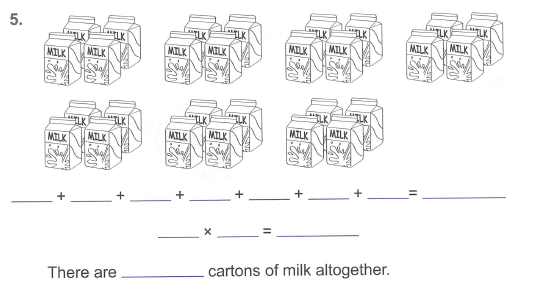
再进行抽象化解题训练。

最后，进行到实用部分，讲解应用题的做法。

先练习有提示的算式，再练习没有提示的应用题。大量贴近生活的题目设计让孩子在现实生活中感受数学，加深对数学的理解。

同样一个知识点，它绝不会反复停留在同一类题目，而是不断变化题型，递进难度，让“刷题”这件事变得非常高效。

“新加坡数学”系列教材非常重视孩子计算的过程，虽然有的计算过程粗看起来比较慢，但是每一步都能够激发孩子的思考，孩子们能够受到启发，做到举一反三，拒绝题海战术。

曾经有位使用过“新加坡数学”的家长说：如果只是为了考试竞赛，同一类题型不一定需要掌握那么多层次的解法。而“新加坡数学”会不断启发孩子，去思考和尝试新的解法，同时也给孩子传递了很重要的信息：

●  问题的解决方法，永远不止一个；

●  也永远不要认为自己100%精通了某类问题，因为它的难度和复杂度都会发生变化；

这就是训练技巧和培养思维的区别。

前者遇到熟悉的题型会很快就做出来，但题型只要发生一点变化，学生就容易被难住。而后者的优点是不断挑战自己思维的深度、广度和创新度，将来遇到不同类型、不同难度的题型，会更灵活更有胜算。