CIE 数学 FP1 invariant line知识点扩展

同学们，今天我们来看一下今年5月CIE 数学FP1 12卷第7题(d)问：

我们先按常规步骤写一下，从设invariant lines的方程是y=mx开始：

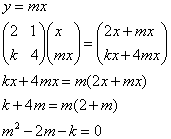
因为有两条不同的invariant lines，所以m要有两个不同的实数值，上面最后的一元二次方程的discriminant要大于0：

这样就做完了，好像很简单的样子呢。让我们来康康答案验证一下：

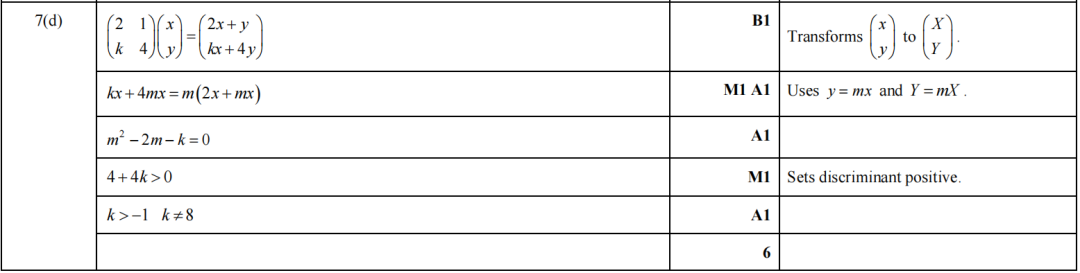
Emm......k>-1是没错，可是为什么后面还有个k≠8呢？

我们先看看k=8的时候到底是什么情况：

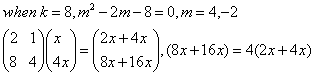
m=4没毛病。再看m=-2：

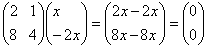
这里就有点疑惑了，这个式子说明k=8的时候y=-2x上的点全都会被矩阵变成(0,0)，倒是也满足y=-2x，可是这已经不能叫“invariant line”（重点是line）了，因为整条线都变成一个点了，而不是像m=4的时候一样变完了还是一条线：

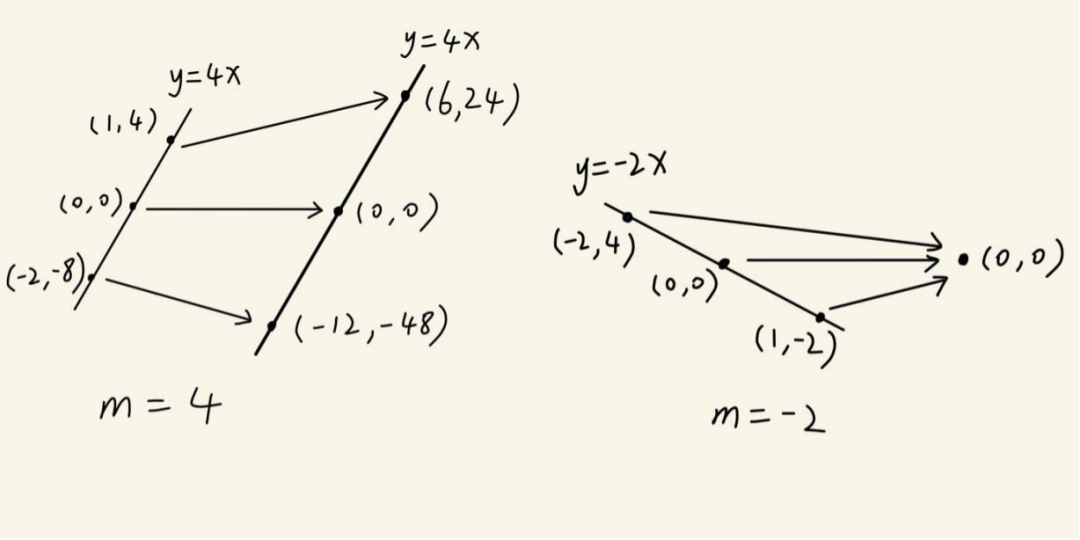
所以，这个时候实际上只有一条invariant line y=4x。

k≠8的原因知道了，可是做题的时候怎么能想到这一点呢？谁会在求出k>-1之后还再去一个一个验证所有大于-1的数是不是满足题目要求呢？这里要给同学们补充一下教材上没讲到的知识点：如果2×2矩阵A的行列式detA=0，那么A只有一条invariant line。这是因为，如果detA=0，那么A的两行成倍数关系：

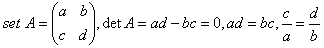
设这个倍数是n，那么A可以写成：

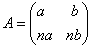
对任意一个点(x,y)，经过A变换之后

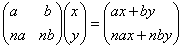
都会变成一个纵坐标是横坐标n倍的点，所以A的invariant line只有y=nx。

当k=8时，真题中的矩阵行列式正好就等于0。所以同学们以后如果再遇到类似的题，只要记得检查一下矩阵的行列式是不是等于0就可以了。