2022 Ross数学营申请通道正式开放
2022年Ross数学训练营已开放申请。为了保持Ross营精神的传承,组委会经过讨论,决定取消线上营。在美国开放两个线下营地,每个营地招收60名新生。
由于疫情防控和出入境管理政策,暂停举办2022罗斯亚洲营,并且受疫情防控和出入境管理政策影响,境外学生可能无法申请美国营。
Ross营申请试题已经公布,老师还给大家带来了保姆级的Ross营申请流程指导,各位数学挑战爱好者一定要收藏起来!
2022 Ross营基本信息
Ross Mathematics Program由阿诺德·罗斯博士于1957年在圣母大学创立,旨在鼓励学生积极探索数学。从1964年到2018年主要与俄亥俄州立大学(Ohio State University)合作,2019年,该项目转移到俄亥俄多明尼加大学,2020-2021年该项目完全在线。
Ross营与PROMYS、SUMaC并称三大美国数学训练营。(点击此处查看2022数学夏令营汇总)Ross营以启发学生自主发现抽象概念,考虑全新的问题,开发以前没有见过的方法,并证明每个答案,不仅要求学生能熟练掌握计算任务,而且为培养批判性思维打下基础,致力于培养学生独立思考的能力和质疑的态度。
■申请时间
● 申请提交截止日期:2022年3月31日(美东时间)
● 选拔并陆续发放录取结果:2022年4月1日(美东时间)起
■营期时间
● 俄亥俄州营(多米克大学)
6月15日-7月27日
● 印第安纳州营(罗斯霍曼理工学院)
6月19日-7月29日
■申请要求:对数学、科学感兴趣且具备一定英文基础的15-18岁学生
■申请费用:$6000
■申请材料
✔ 个人信息-Background
✔ 家长信息-Parent Information
✔ 个人陈述-Personal Statement
✔ 小文书-Short Essays
✔ 申请题-Solutions
✔ 学校成绩单-Transcripts
✔ 推荐信-Recommendation
✔ 附加材料,如简历等-Attachments
■ 申请题目辅导:MathMaster提供入营资格测试辅导,详情可咨询~
2022 Ross营申请题
Ross营申请材料中,申请题Solution是必须要提交的一项材料,随着申请通道的开放,今年的入营试题也已经公布了↓
※申请题目一览

2022 Ross营申请流程01申请材料准备
在Ross营的申请系统中需要提交一下材料,因此同学们需要提前准备好一下材料:
✔ 个人信息-Background
✔ 家长信息-Parent Information
✔ 个人陈述-Personal Statement
✔ 小文书-Short Essays
✔ 申请题-Solutions
✔ 学校成绩单-Transcripts
✔ 推荐信-Recommendation
✔ 附加材料,如简历等-Attachments
更多详细信息可以登陆官网查看
https://rossprogram.org
02注册Ross营申请账号并登陆
进入申请页面
https://apply.rossprogram.org
使用邮箱注册,密码会以邮件形式发送至邮箱:
邮箱与密码登录,正式进入申请系统。
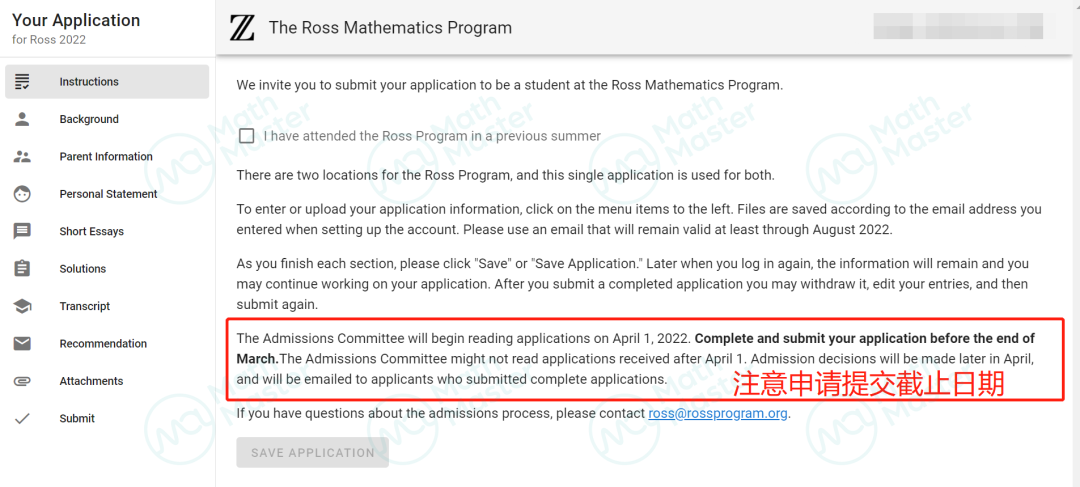
03提交申请材料
左侧导航栏是需要申请者需要提交的材料,根据其要求上传填写个人信息、父母信息、个人陈述、小文书、申请题目解答、推荐信等内容,完成后即可提交申请。
(1)个人陈述
个人陈述需要围绕官网提供的问题进行讨论,包括对于数学的兴趣、参加Ross营的目标,以及在数学之外的兴趣与爱好。
(2)小文书Short Essays
小文书分为projects, competitions, other programs, books and websites, future goals, collaboration, other coursework, being away from home这八个方面,申请者需要在这一部分展示自己与数学相关的学术活动、赛事、阅读以及对未来专业的思考。
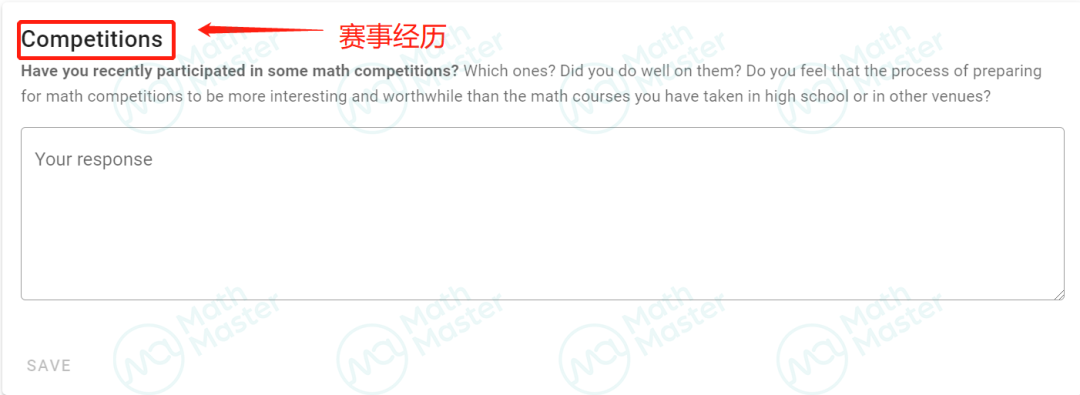
其中Competition一栏下面需要填写数学相关赛事的经历,无论是AMC/AIME/Euclid/UKMT等都是非常重要值得同学们填写进去的内容!
在这部分申请者不仅需要指出自己参加了哪个赛事,还要思考“是否觉得准备数学竞赛的过程比在学校或其他地方学习的课程更有趣,更有价值”等相对更主观的问题。
(3)申请题解答Solution
2022年Ross申请试题已经公布,申请页面可以下载(文末可以领取2022Ross营完整版试题PDF)
提交材料的过程中需要注意:
* 每道题的解答必须以单独的PDF格式上传。
*必须使用PDF文件格式。如果您文件是其他格式的要将其转换为PDF,检查转换后的文件是否可读,然后上传该PDF。
*招生委员会并不是需要申请者在最短的时间内写出快速的答案,而是要有清晰可读的数学说明,包括你的思考探索、猜想和证明的过程。