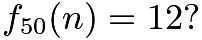在2021-2022年的AMC赛季中,S老师发现了一个很普遍的现象——很多同学有着一颗想要冲击AMC10/12高分的壮志雄心,但一看到题目,又觉得难度太高,倍感力不从心。
但是,AMC真的有那么难吗?难道没有破解之法吗?为了给大家答疑解惑,S老师今天特地请来MathMaster的F老师指点迷津,想要知道怎么让AMC10/12 这块“拦路虎”变成未来的“垫脚石”吗,快来听一听F老师的锦囊妙计吧!
了解赛事— 你真的了解AMC10/12吗 —
《孙子兵法》有言:“知己知彼,百战不殆。”想要在AMC 10/12中取得令人艳羡的高分,了解赛事便是重中之重。
那么,什么是AMC10/12呢?
其实,AMC10/12已经达到了业界所公认的Intermediate Level of Math Competetion,简单来说,它是一个中级的数学竞赛。
“中级的数学竞赛”,这句话应该如何理解?对此,F老师从专业角度详细解构了这句话中的两层含义:
第一,AMC10/12的确是一个数学竞赛,并且是一个选拔性的考试而非合格性考试。
第二,尽管AMC10/12是选拔性考试,但其并不是Olympiad Competition,所以,从某种程度上来说,目前的AMC10/12还不具备和数学奥林匹克相当的专业性。
因此,相比学校内的任何数学考试来说,AMC10/12更灵活,技巧和知识更超前。同时,AMC10/12比AMC8的难度也要大得多。但也正是由于它不具备专业性,所以考生具有更广阔的发挥空间——不需要全部使用专业的数学竞赛知识解决问题,而是可以从课本、课外内容得到灵感和启发,从而举一反三,灵活地处理题目、突破难点。
明确现状— AMC10/12与MO壁垒变薄 —
尽管如此,AMC10/12仍让很多考生望而却步。答案很简单,一个字——“难”!
在一定程度上,F老师也认可这种情况,他表示:“的确存在难度。而且,虽然每年的AMC10/12题目难度有所不同,但能够看到的是,Math Competition 和Olympiad Competition(即MO)之间的壁垒逐渐变薄,几乎已经被打破。”
提及Math Competition 和Olympiad Competition之间的差异,为了更具象化形容,F老师拿了选拔乒乓球队做比喻,“一个像是上海青运会选拔赛,而另一个则像奥运会选拔赛。”
两相对比,难度差异可见一斑。此外,除去难度上的差异,学生在这两种赛事上遇到的对手也有不同。毕竟山高险峰多,Olympiad Competition中,对手的实力会更强劲。且作为一种技能型的选拔考试,Olympiad Competition的考试内容更偏向“能力”而非知识,正因如此,学生需要具有很强的技巧性和理解力。
“如果学生以一个Olympiad Competition选手的标准来要求自己,那么AMC10/12对于他来说,就是小菜一碟了。”F老师如是说。
为了能更好地阐述“AMC10/12与MO的壁垒逐渐变薄”是什么意思,F老师拿出2021年秋季AMC12的第20题为求知若渴的大家举例:
Foreach positive integer ![]() ,let
,let ![]() betwice the number of positive integer divisors of
betwice the number of positive integer divisors of ![]() ,and for
,and for ![]() ,let
,let 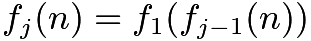 .
.
“尽管你的书本功夫十分扎实,但也有可能遭遇瓶颈。毕竟,这个题目并不是一个聪明的孩子通过对书本的细致理解,就能够举一反三,且能在考场紧张的时间里迸发灵感的。”
对于这样一道涉及了最基本的Hardy数论中的函数的变种,又结合了函数迭代、映射形式的函数理解等知识的题目,F老师继续分析道,“我们在最朴素的人类认知规律下分析,这个题目的公式是新的,迭代的思想是新的,且Counting的问法是难的。”
所以,如果想要临场解决这种级别的题目,单靠纯粹的AMC10/12训练可能还不够。考生需要足够的“知识输入”,需要对初步的Olympiad Competition问题进行深入思考,并且不惧怕失败、通过失败来总结出自己的经验,通过纠正错误得到仅属于自己的数论直觉。
“没有一本合格性考试的教材中有任何一道题、一句话,能够帮你达到这个目的。”F老师的言语中肯,迸发出睿智的精光。
洞悉方向— 如何取得AMC10/12高分 —
如果你想要在AMC10/12中拿到高分,就得以一个MO选手的标准来严格要求自己。
从F老师多年的经验来看,仅仅学习和训练“所谓的”AMC12级别题目的学生(F老师说,这里加“所谓”,是因为今年AMC12的难度提升得非常夸张,甚至已经不容易界定什么题目叫做AMC12难度了,似乎它最终考得多难都不太令人惊讶),很难在考场的高压之下发挥到最好。
所以,在这种现状下,考生们最好的方法就是学习基本的Olympiad Competition数学知识。
F老师建议,要想训练出学生的能力,就得脱离功利且单调乏味的训练,真正让学生形成自己的数学直觉,既“会用”又“会讲”。具体来说,就是对数学公式、定理能有严谨的证明和使用的能力(抽象思维),也具有把公式和定理用自己的话“形容”出来的一种反刍(具象思维)。
除此之外,F老师还拿出芝加哥大学的黎曼几何期末考题作为例子(F老师形容,这种考题属于是学了Lie代数以后那种味道的计算),提醒考生们要保持良好的计算态度、能力和计算方法。“本质上,数学考试都会落实在计算上,哪怕你学到了黎曼几何,非交换里的K-Theory,它们的期末考试中仍然会有一些计算题的。”F老师说。
倾囊相授— F老师是如何教学的 —
为了帮助学生在AMC10/12中得到好成绩,F老师以自己的学习心得和多年教学经验为基础,形成了一套独特的教学方法。而这种教学方法成果斐然,在他所带2020年秋季入校班和2021年寒假AMC10集训营中,多名学生成功晋级AIME,展现出不俗的实力。
焦点问答
Q:您提到,会以更难的程度来要求学生,具体体现在哪些方面呢?
A:在上课讲完知识点后,我会通过一些简化版的Olympiad Competition竞赛题,让学生掌握所需知识的用法,让他们理解如何去使用这些知识。我希望能够通过这些有一定难度的题目,去拓展学生们的思维,让他们明白,数学不仅只有知识,也有技能。
Q:可以解释一下什么是Olympiad Competition级别的训练或者题目吗?
A:中文意思就是奥林匹克级别的题目,可以理解为完全建立在中学数学知识的基础,对更深刻的大学数学知识的背景进行挖掘的这类问题,比如AMC10/12个别最后3题、AIME个别的最后5题和各个国家的奥林匹克竞赛题,比如USA/JMO美国数学奥林匹克的问题就是Olympiad Competition级别的题目。
Q:您通过什么样的方式培养学生的数学灵感?
A:我认为,考场上的灵感需要在平时多训练,练出一定的“手感”。比如,证明定理就是一个很重要的方式。所以,在我的课堂上,我会让同学来证定理。先让学生们自己算一遍,我再来讲一遍,通过对比,让他们体会思维上的差异,慢慢地具有数学上的“灵感”。
Q:您所说的“不功利的训练”,是什么样的训练呢?
A:我希望,学生们在做题时不要只用原理和定理往里套,数学题并不是僵化的,而会“七十二变”。如果一直拿“套路”来套的话,肯定是不行的。对于我来说,假如我要讲全等,那么我一定会拿出一些学生没见过的题,让他们产生思考,从而推进掌握,在课后作业中,我也会布置不一样的知识点。这样的话,学生会有新鲜感,也会减少套路的使用,从而培养他们解决问题的态度。
Q:您是如何让数学教学更生动的?
A:我的课堂不是单纯地灌输知识,我也会和同学们进行讨论。比如,在课堂上,我经常向学生提出问题,询问他们这样做是否正确,有时候,我甚至会故意给出错误的答案来考他们。
Q:遇到特别难的题,您是如何讲解的?
A:这种情况很常见。我在备课中,经常遇到一些对于学生来说比较困难的题目。对此,我会找出有类似核心理念的、较简单的题目(尽管有些知识点是不同的),先让学生理解这个题目用到的思路,再引导他们试着去解决这道比较难的题目。
在采访将要结束时,F老师说:“在后面的课程设计和教材编写上,我也在尝试做尽可能多的修改,一方面贴近各个阶段的学生实力,另一方面,也把枯燥的、高思维深度的内容生动地表达出来,希望让学生们真正喜欢上数学。”
近年来,AMC作为一块“敲门砖”,却越来越难以让普通人拿得动,但同时也恰恰证明了其含金量在升高。
所以,面对AMC和MO的壁垒逐渐被打破的现状,“对于真正志在冲击AMC10/12高分甚至是AIME晋级USA/JMO的同学来说,一定要做好准备,拿出十足的热情,投入十足的精力。”最后,F老师对大家报以真诚祝愿。