引言
自 2022 年 3 月中旬以来,上海每日新冠确诊病例和无症状感染者的数量一路飙升。4 月 5 日当日,新增本土新冠肺炎确诊病例 311 例和无症状感染者 16766 例(图 2)。目前疫情规模已经超过了武汉,并且还没出现拐点,上海的防疫到了最艰难的时刻。
上海曾是全国抗疫肺炎的模范,为何如今却成为疫情的重灾区?专家认为原因分客观和主观两方面。客观方面,奥密克戎变异株的传染性和隐蔽性较强,该变异株的传播能力比奥密克戎原始株高 30% 左右,而且所造成的感染大部分是轻症或无症状感染,能够逃过常规核酸检测,所以隐蔽性更强,这也给精准防控带来了困难。此外,上海是人口众多的国际大都市,国内外的贸易和人员往来太密切而复杂。主观方面,防疫人员防控意识松懈,对防疫过于自信,没能早发现早制止。当意识到疫情的严重性时,病毒早已全面蔓延开来,甚至连累了全国其它很多城市。此外,还有很多群众不配合防控也给防疫带来很大的挑战。例如有人初筛阳性,被通知要求核酸复查后却拒不配合,而是乘坐动车再转乘坐网约车回家了。
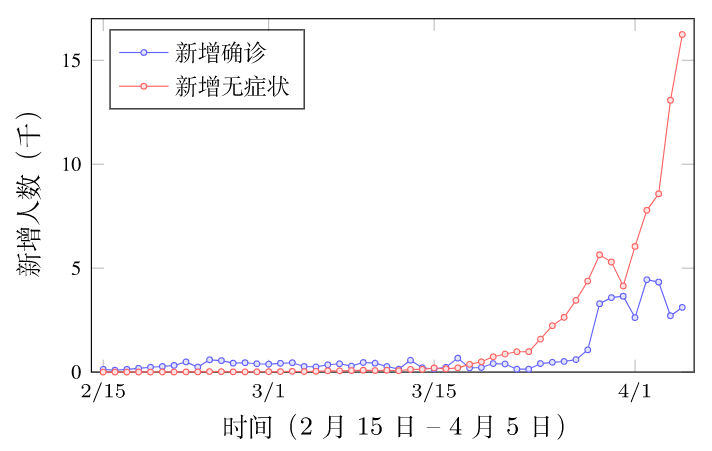
图 2: 上海本轮疫情走势
但值得庆幸的是,奥密克戎虽然传染性强,但致病毒性降低。很多感染者只是被影响到上呼吸道,基本没有症状。而且,上海是全国疫苗接种率最高的城市之一。因为疫苗的保护,人体免疫力增强,即便被感染,也绝大部分是轻症和无症状感染。
问题
图 2 是 2 月 15 日 - 4 月 5 日上海每日新增本土确诊和无症状人数。从图中可以看出 3 月 15 日之后,数据不断上升。将本土确诊和无症状人数合并为感染人数,表 1 给出了以 2 月 15 日为起点上海最近二十天( 3 月 17 日 - 4 月 5 日)累计感染人数。例如表中 3/17 对应的数据 2626 表示 2 月 15 日至 3 月 17 日每日新增确诊和新增无症状人数的总和。
表 1: 上海最近二十天累计感染人数
| 日期 | 累计 | 日期 | 累计 |
|---|---|---|---|
| 3/17 | 2626 | 3/27 | 17315 |
| 3/18 | 3018 | 3/28 | 21804 |
| 3/19 | 3534 | 3/29 | 27781 |
| 3/20 | 4311 | 3/30 | 33438 |
| 3/21 | 5218 | 3/31 | 37948 |
| 3/22 | 6213 | 4/01 | 44261 |
| 3/23 | 7209 | 4/02 | 52494 |
| 3/24 | 8837 | 4/03 | 61512 |
| 3/25 | 11117 | 4/04 | 74871 |
| 3/26 | 13801 | 4/05 | 91438 |
请根据表中数据,建立模型描述上海本轮疫情累计感染人数(表 1 中的数据)的变化规律,并对未来两日内每日新增感染人数作出预测。
模型
复合增长
对于一个相对封闭的城市,每日新增的本土感染病例都是被之前本土已感染病例传染的。当累计感染人数远小于城市总人口时,每日新增病例应该与累计感染人数成正比。上海目前累计感染人数约为 10 万,远小于上海 2500 万的总人口。因此,上海每日新增病例应该与累计感染人数成正比,或者说上海病例日增长率应该近似为一个常数。这就和固定利率的银行存款问题类似,如果我们用 Y0表示 3 月 17 日累计病例数(相当于本金),那么 3 月 18 日的累计病例数(Y1)=3 月 17 日累计病例数(Y0)+3 月 18 日新增病例数(相当于利息)。当天新增病例数等于前一天累计病例数*增长率(相当于利率),所以有
![]()
其中r 为日增长率。同理可以得出第n 天累计病例数为
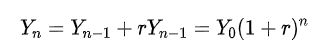
接下来我们需要验证上海的病例日增长率r 是否为常数。第 t+ 1 天病例日增长率可表示为
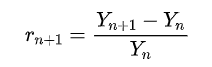
其中 Yn+1-Yn表示第 n+ 1 日新增病例数。例如,3 月 18 日的增长率为
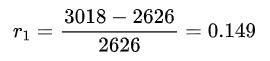
其中 2626 和 3018 分别为 3 月 17、18 日的累计病例数(表 1)。类似地,我们可以计算得到上海近二十天累计感染人数日增长率(表 2)。
表 2: 累计感染人数日增长率
| 日期 | 日增长率 | 日期 | 日增长率 |
|---|---|---|---|
| 3/17 | -- | 3/27 | 0.255 |
| 3/18 | 0.149 | 3/28 | 0.259 |
| 3/19 | 0.171 | 3/29 | 0.274 |
| 3/20 | 0.220 | 3/30 | 0.204 |
| 3/21 | 0.210 | 3/31 | 0.135 |
| 3/22 | 0.191 | 4/01 | 0.166 |
| 3/23 | 0.160 | 4/02 | 0.186 |
| 3/24 | 0.226 | 4/03 | 0.172 |
| 3/25 | 0.258 | 4/04 | 0.217 |
| 3/26 | 0.241 | 4/05 | 0.221 |
从表中不难看出,日增长率基本在 0.2 上下波动,并且基本在 0.15-0.25 之间,因此可以认为日增长率为常数。我们可以用 3 月 18 日累计病例数 2626 作为模型参数Y0的估计,用表 2 中 19 个日增长率的算术平均值作为模型参数r的估计:
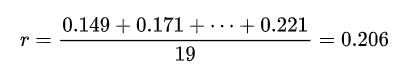
由此可得图 3 中的红色预测曲线,预测结果均方根误差(预测值与观测值偏差的平方和与预测次数比值的平方根)为 1333。预测给出 4 月 6、7 日的新增病例数分别为 19039 和 22963。
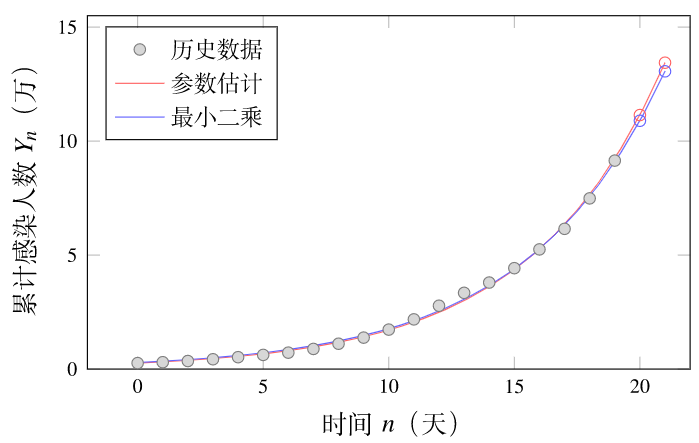
图 3: 复合增长模型预测结果
当然也可以根据表 1 中的数据直接应用最小二乘法拟合得到模型参数: Y0= 2884, r= 0.199 拟合曲线见图 3 中的蓝线,相应的预测结果均方根误差为 1197。预测给出 4 月 6、7 日的新增病例数分别为 18097 和 21700。
指数增长
复合增长模型假设了病例数量是以天为单位增长的,但实际上病例数量在每一小时、每一分、每一秒都在增长。如果将每天的时间细分为 等份,累计病例数在每一个等份时间的增长率为 x= r/m,则第 t天的累计病例数可表示为
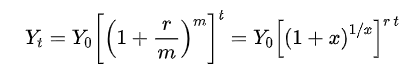
将上式方括号中的项定义为函数 f(x)= (1+x)^1/x。随着时间无限地细分, m将无限增大,而 x将趋于 0。 f(x)随着x→0 的变化过程见表 3。
表 3: f(x)的根限值
| x | 0.1 | 0.01 | 0.001 | 0.0001 | 0.00001 |
|---|---|---|---|---|---|
| f | 2.59 | 0.705 | 2.716 | 2.718 | 2.718 |
从表中不难发现,当 x 逐渐趋于 0 时, f(x)也逐渐趋于一个常数:
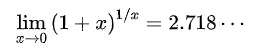
这个常数被定义为自然底数 e = 2.718…… ,它是重要程度不亚于π 的另一个无理数。因此,第 t天的累计病例数可表示为以下指数增长模型:
![]()
这就为什么像大模头这样的专家们在谈论疫情时,经常会说“呈指数级增长”。实际上,现实世界中很多数量的增长都呈现类似的规律,比如生物种群的数量增长。通过最小二乘法,我们可以拟合出指数增长的模型参数: Y0= 2884, r= 0.182。拟合曲线见图 4,相应的预测结果均方根误差为 1197。
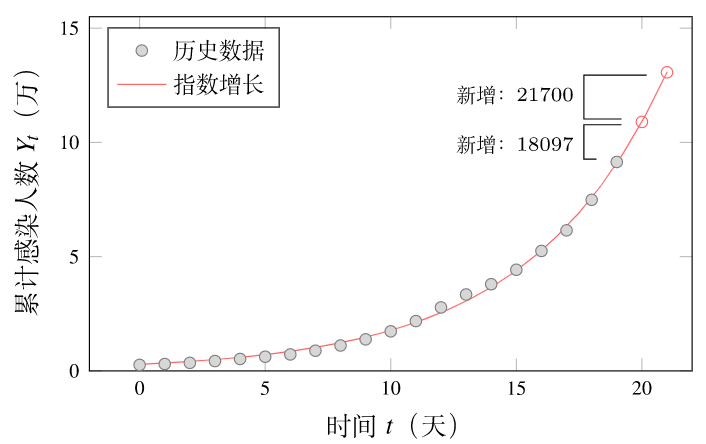
图 4: 指数增长模型预测结果
预测给出 4 月 6、7 日的新增病例数分别为 18097 和 21700。指数增长模型给出的结果与最小二乘法拟合得到复合增长模型的结果一致。这说明在短时期内,复合增长模型已经足够说明问题。这一点很重要,特别是当我们在中学知识范围下讨论这个问题时。
结论
自 2022 年 3 月中旬以来,上海每日新增本土确诊和无症状人数一路飙升。根据 3 月 17 日 - 4 月 5 日累计感染人数,本文先建立了复合增长模型。在此基础上,考虑到病例的增长并不是逐日进行的,本文将每天的时间进行细分。在无限细分的极限条件下,复合增长模型转变为了指数增长模型。指数增长模型给出的结果与复合增长模型的结果一致:上海的累计新冠病例数量正在以 20% 的日增长率增长,4 月 6、7 日的新增病例数将达到 1.8 万和 2.2 万左右。
需要注意的是,本文的模型预测结果是建立在 4 月 6、7 日不出现拐点(即累计感染人数仍按照之前二十天的规律增长)的假设前提下得到的。
参考资料
[1]国家和省市卫健委, 疫情实时大数据报告, 2022/4/5:https://voice.baidu.com/act/newpneumonia/newpneumonia
[2]刘来福, 高中数学建模, 北京师范大学出版社, 2019