怎么证明万有引力？

大家想必都听说过牛顿和苹果树的故事。牛顿为了躲避瘟疫回到乡下，睡在苹果树下，结果被苹果砸到。牛顿就想到：“为什么苹果都是往下掉，而不是往天上掉呢？”进而提出了万有引力定律：物体彼此之间都互相的吸引力，这个力和两个物体的质量都成正比，和两个物体的距离的平方成反比。也就是：

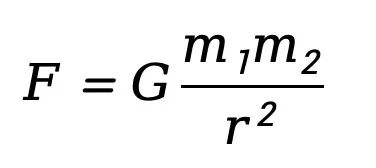
牛顿当时并没有得到比例系数G的值。而且，为啥一定就是所有的东西之间都有引力呢？有没有可能是只在地球和别的物体之间存在吸引力呢？

01卡文迪许扭秤实验

为了证明万有引力的存在，并且测量万有引力常数的大小，卡文迪许设计了扭秤实验。

卡文迪许在一个密闭的房间内，将小金属球系在长为6英尺木棒的两边，并用金属线悬吊起来。再将两个350磅的铜球放在相当近的地方，以产生足够的引力让哑铃转动，并扭转金属线。

在金属线上，卡文迪许放置了一面老师子。哑铃转动之后，带着镜子转动，从而让远处射向镜子的光线，反射到墙上的光点位置也跟着发生变化。

就算离得很近，铜球和小金属球产生的作用力依然非常小，因此卡文迪许设计了三重放大作用，来放大球和球之间的万有引力的影响。第一重是通过放置两个球，两边各自产生作用，把力的左右转变为力矩作用，从而将力臂作为第一重放大杠杆。

第二重是将金属线的转动，通过反射镜放大为二倍，将反射转角作为第二重放大杠杆。第三重就是通过光线传播的时候，角度转变产生的距离等于弧度变化值乘以半径，将传播半径作为第三重杠杆。

02万有引力得到证明

卡文迪许的实验设计的十分精巧，但是感兴趣的同学可以自己试一试，越是精巧的实验就越容易遇到各种问题产生误差，导致失败。卡文迪许的实验也重复了很多次，才得到了满意的结果。比如卡文迪许为什么一定要放在密闭的房间里，就是因为一点小小的气流干扰，就可能导致实验完全失败。

扭秤实验最后成功观察到了金属丝的转动，从而论证了万有引力的存在，并且测量除了精度相对较高的万有引力常数。聪明的读者们可以开动脑筋，还能不能想到啥别的证明万有引力存在的方法吗？感兴趣的读者可以私信老师进行交流。