AMC12题选：“时间困难”的问题——起点很近，终点很远

有计划参加今年的AMC12的学生，从暑假开始就必须开始做备赛规划了。我近期将挑选几道AMC12真题做一些分析和点评，希望能对大家有所启发和思考。

本文是这个系列的第五篇文章。这次我选的题目如下：

给定一个正12边形，任意选择12边形的两个顶点连一条线段。从这些线段中随机选择3条线段，这3条线段能构成一个面积为正的三角形的概率是多少？

这道题的逻辑很简单。首先，可以连成的线段一共有66条——这个数量小学生都可以算出来。其次，从66条线段中随机选择3条线段，能否构成面积为正的三角形，取决于最长的线段长度是否（严格）小于另外两条线段的长度之和。

从上面的分析可知，这道题的逻辑复杂性只是小学程度，为什么在AMC12中会被排在第24题？先别急，只要再往下想一步，你就马上能明白其中的原因。

为了判定所选择的三条线段是否能构成三角形，我们需要知道这66条线段的长度分别是多少。然而，由于12边形不是常见图形，这些线段的具体长度都需要临时计算。

如果把这66条线段按长度分类，即长度相等的线段归为一类，一共可以分成6类。我们按长度从小到大分别记它们的长度为L₁,L₂, ...,L₆。其中，长度为L₁的线段是12边形的边，其余线段都是12边形的对角线。此外，长度为L₆的线段有6条，其余5类线段的数量都是12条。下图通过半个12边形的图形显示了6类线段的状况。

接下来我们分别计算线段长度的具体值。不妨设L₁=1。

长度为L₂的线段与两条长度为L₁的线段构成一个等腰三角形，且顶角的度数为150°（因为正12边形的内角都是150°）。我们可以用余弦定理求出L₂的数值，如下图。

长度为L₃的线段与三条长度都是L₁的线段构成一个等腰梯形，如下图。把梯形的下底分割成三段，并注意到△ABC是直角三角形，且∠A=60°。利用这个关系可求出L₃的数值。

长度为L₄的线段与四条长度都是L₁的线段构成一个五边形，如下图。其中，△ABC是腰长为L₂、顶角度数为120°的等腰三角形。据此可求出L₄的数值。

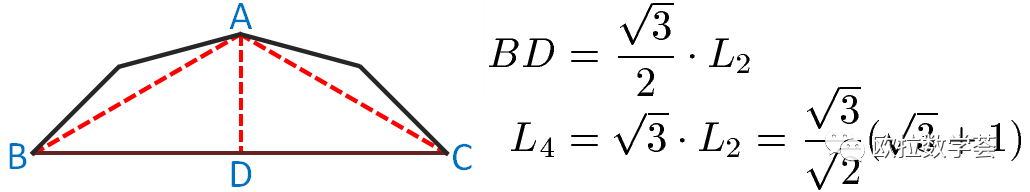
长度为L₅的线段与五条长度都是L₁的线段构成一个六边形，如下图。其中，△ABC是斜边长度为L₂的等腰直角三角形。据此可求出L₅的数值。

长度为L₆的线段与六条长度都是L₁的线段构成一个七边形，如下图。其中，△ABC是直角边长度为L₃的等腰直角三角形。据此可求出L₆的数值。

上面求出的L₂~L₆的数值仍然是表达式，不方便判断相互之间的大小关系，所以我们希望能求出它们的小数近似值。但L₂和L₄的表达式中都有无理数出现在分母的位置，不方便做计算。为此，我们把L₁~L₆的数值都乘以根号2，从而可以回避涉及无理数的除法运算。

下面的表格列出了乘以根号2以后的L₁~L₆的精确到小数点后两位的近似值。

根据这些数值，我们可以判定怎样的三条线段不能构成面积为正的三角形。

1. 有两条线段的长度都是L₁，第三条线段的长度为L₃~L₆。

2. 有两条线段的长度都是L₂，第三条线段的长度为L₆。

3. 其中两条线段的长度分别为L₁和L₂，第三条线段的长度为L₄~L₆。

4. 其中两条线段的长度分别为L₁和L₃，第三条线段的长度为L₅~L₆。

以上是不能构成面积为正的三角形的所有可能情形。接下来分别求每一种情形下选择线段的方式的数量，就是标准的计数问题了。

情形1：由于从12条线段中选择2条线段的不同方式有12×11÷2=66种，所以此情形下选择三条线段的不同方式数量为66×(12×3+6).

情形2：此情形下选择三条线段的不同方式数量为66×6.

情形3：此情形下选择三条线段的不同方式数量为12×12×(12×2+6).

情形4：此情形下选择三条线段的不同方式数量为12×12×(12+6).

把上面四个表达式相加得(66+12×12)×48=210×48.这是不能构成面积为正的三角形的三条线段的选择方式的数量，而题目问的是概率，所以还要除以选择任意三条线段的所有方式的数量，即66×65×64÷(3×2×1)=11×65×64.所以不能构成面积为正的三角形的概率为210×48÷(11×65×64)=(7×9)÷(11×26)=63/286,可以构成面积为正的三角形的概率就是1-63/286=223/286.

回顾整个解答过程，关键问题在于确定所有线段的长度——一共有多少种不同的长度，每种长度的线段有多少条。在求长度的数值时，需要用到不同的几何公式，例如勾股定理、余弦定理。

如果我们单独看每一步的计算，都不涉及复杂的公式和处理方法，但由于计算步骤非常多，要做到完全不出错是很不容易的。

这样一道题，如果给一个小时的解题时间，可能很多学生都能做出来；如果只给半个小时，能做出来的学生就少了很多。能在15分钟内做出来的学生，我相信是凤毛麟角。

这类题目，最大的困难就在于解题时间的限制——你很容易想明白应该怎样解答，但要得到最后的答案，你必须非常有耐心地完成一个又一个的步骤，非常小心地确保每个步骤都不出错。在时间宝贵的考场上，这对学生的抗压能力是很大的考验。

我留作练习的同样是一道“时间困难”的的真题。题目如下：

记G为所有具有以下形式的多项式P(z)构成的集合：

其中c₁,c₂, …,c_n-1都是整数。已知P(z)的根各不相同，且所有根都是“整复数”，即形如a+ib的复数，其中a和b都是整数。请问G中一共有多少个元素？

这道题用到的性质并不复杂。首先，由于所有系数都是实数，所以P(z)的复数根都是成对出现的共轭复数；并且，只要我们选择整复数作为P(z)的根，就可以保证P(z)的所有系数都是整数。

其次，常数项50是关键的条件。P(z)的所有根的乘积应该等于50或者-50。因此，P(z)的每个实根的绝对值都必须是50的约数，每个复根的模的平方也必须是50的约数。

这道题的困难在于，P(z)的次数有多种可能性。我们必须对不同的次数分别讨论P(z)的根的情况，不能有任何遗漏。事实上，在这个问题中有些情况就是特别容易遗漏——别忘了，你并没有一个小时的时间慢慢检索，找遍每一个角落。不过，反正现在不是在考试，你不妨给点耐心把题目做完，然后想想这样一道题放在AMC12的第25题是不是恰如其分吧。