作为剑桥大学招生考试中心于 2016年设立的本科入学测试,TMUA更加侧重较为基本的数学思维和推理技能,也是包括伦敦政经、杜伦以及谢菲尔德等十所高校所认可的重要参考指标之一。
其中 TMUA包含 A、B两份试卷,每份试卷都是 20道选择题,不能使用计算器和字典,考试时间均为 75分钟,A、B两份试卷考察的侧重点不同。本篇将由老师就TMUA的 A卷与Alevel涉及考点的异同比较作简要分享,还请详读。
卷面设
题型差异
『异同概述』
两者间的相同点之一是 TMUA的 A卷考察知识点大都是纯数前段知识点,并不会出现超纲的情况。而其不同点则是在题目形式上,TMUA在综合性和灵活性上更加突出。

来源:2023年剑桥大学官网 TMUA认可院校
具体知识点范围则是微积分的计算、几何意义、直线的两点式、点斜式、直线和圆的位置关系、三角函数的性质、三角形的性质、二项展开式、等差等比数列、余数定理以及三次函数的图像性质。单从知识点上看,对于大部分考生来说都是比较熟悉的,但深挖后的细节与联系其实不容小觑。
而 Alevel考察时是以章节为单位,卷面题目会把该章知识点分成若干小问,相反,TMUA则会将涉及的知识点综合成一个问题。
『真题对照』
比如在 Alevel学习解一元二次方程,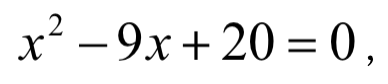
使用“十字相乘”,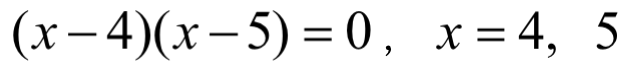
下面对照 2018年 TMUA的 A卷第 15题

来源:2018年 TMUA卷 A第 15题
这是一道解方程的题目,但并不是一元二次方程,以下是化简过程

注意此处题目的要求,需求出根的和,也就是要把求出来的根都加在一起才是答案。
再比如 2020年 A卷 15题,也是一道解方程的题。理综教研部温馨提示:只要是解方程,不管什么形式,都逃脱不了二次方程。大家也可以尝试对照化简。

来源:2020年 TMUA卷 A第 15题
接下来是积分的例题,首先可尝试回想纯数中的积分内容。第一个要求是为求不规则图形的面积,而学习了最常用的幂函数积分公式。第二则是为求近似面积而学习了梯形法则。积分的运算在 TMUA中通常会出现在前三题的其中一题,该题得分率较高,以下是例题参考。

来源:2018年 TMUA卷 A第 1题
对于积分的变换,如下题:

来源:2018年 TMUA卷 A第 12题
虽说涉及积分,其实是解方程组:
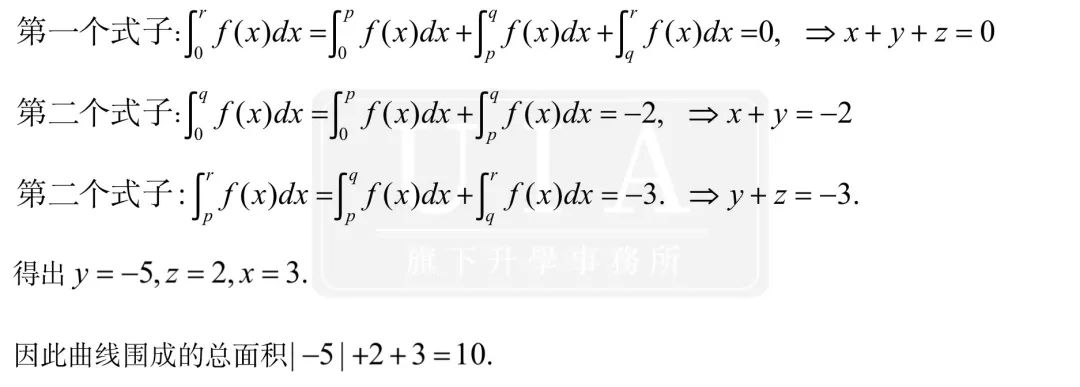
以下是积分与函数图像的平移相综合的例题:

来源:2019年 TMUA卷 A第 16题
此处涉及到函数的平移,注意平移的规则是“左加右减,上加下减”,不仅函数图像可以平移,被积区间同样也可平移。
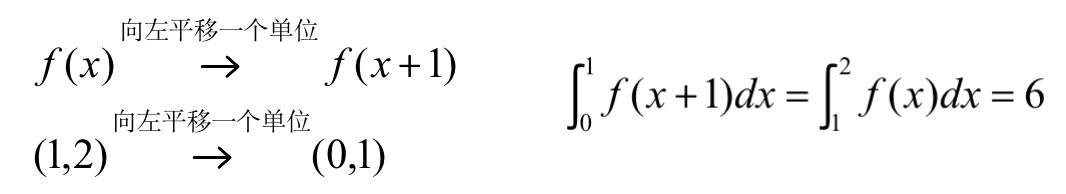
(更易理解的方式可选择换元变形,令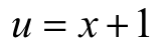 。此处涉及到 P4内容,已学过的学员可尝试求解)
。此处涉及到 P4内容,已学过的学员可尝试求解)
因此可继续求得
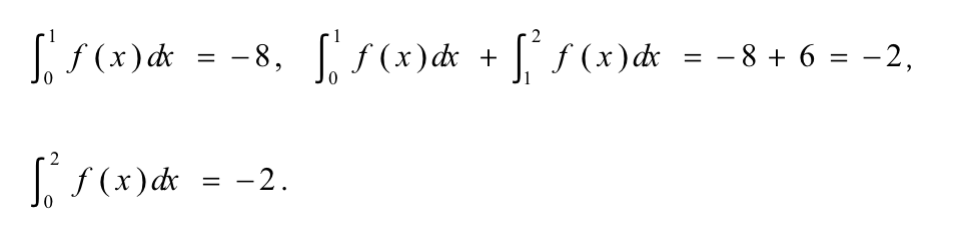
此处涵盖两大知识点的多种考法,解答 TMUA时,需运用联想与适当变形,把 TMUA的题目与之前学过知识点和对应的解题方法相联系。比如看到三角形,不管题目如何设置,首要考虑正弦定理、余弦定理和三角形的面积公式。看到微分,则要想到一次导数和函数图像增减性的关系、二次导数和函数最值的关系、切线以及法线。
有些学员可能觉得会有些畏难情绪,其实认真备考,按照理综教研部的集训要求落实下来,横向比较 Alevel数学能够拿到 A*,TMUA中初级目标为 20道题目答对 12道,此处对应纯数知识点。而剩余部分则是第二阶段需要搭配内部真题以及压轴题集重点攻克,以超越 Alevel的基础端,真正突破自己,在综合性与灵活性并进的 TMUA考试中绽放光彩!