AMC竞赛是什么:
AMC是美国数学竞赛的简称,全称为American Mathematics Competitions。AMC由美国数学协会(MAA)主办,是美国著名的数学竞赛之一,也是全球最大的数学竞赛之一。
AMC10 也是公认的入门级竞赛。如果学生们想测试一下自己的水准,AMC10一定是学生们的首选。
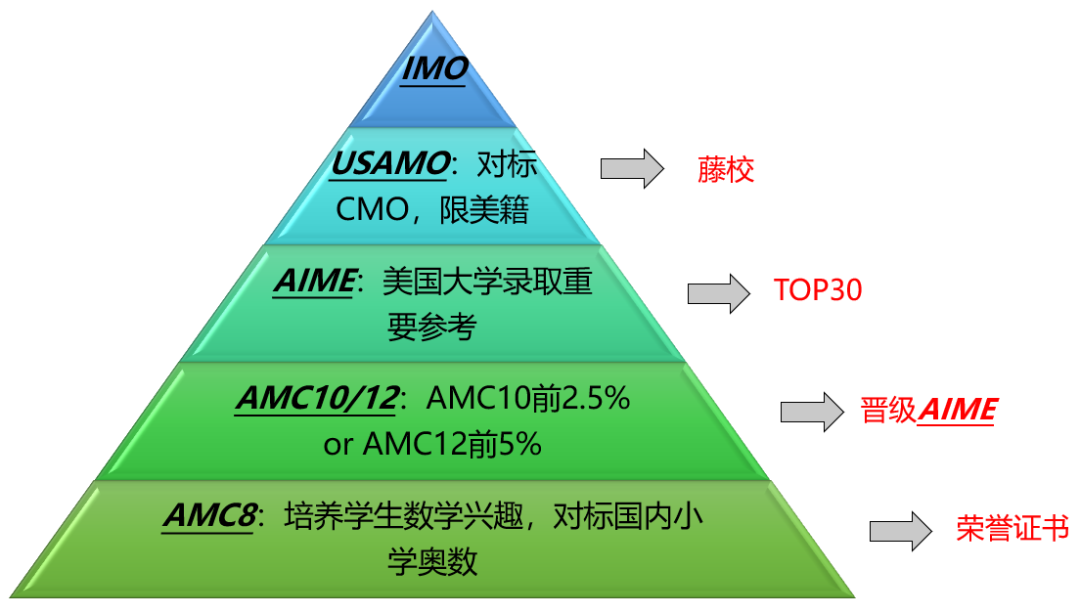
AMC竞赛分为三个级别:AMC8、AMC10和AMC12。AMC8适合8年级及以下的学生参加,AMC10适合9-10年级的学生参加,AMC12适合11-12年级的学生参加。竞赛成绩可以用来申请美国数学奥林匹克竞赛(USAMO)和国际数学奥林匹克竞赛(IMO)等数学竞赛活动。
参加AMC竞赛可以帮助学生锻炼数学思维能力,提高数学解题能力,增强自信心和竞争意识,也可以为将来参加数学竞赛和申请名校提供较好的背景。
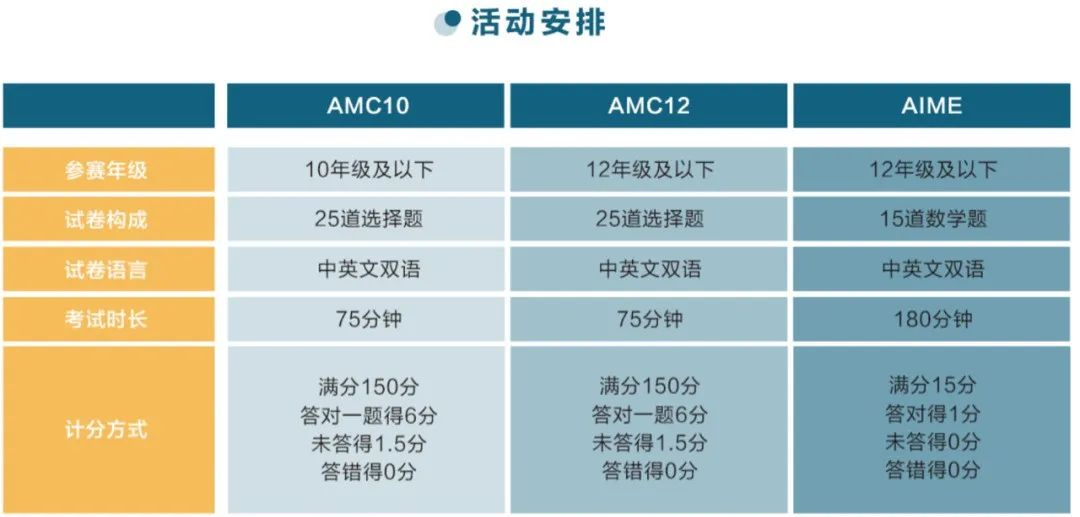
赛制设置
AMC10赛制设置
参赛资格:10年级或以下,且年龄不超过17.5岁
竞赛时长:75分钟
竞赛题型:25道单项选择题
竞赛时间:
AMC 10A卷考试时间:2023年11月8日
AMC 10B卷考试时间:2023年11月14日
计分方式:答对一题得6分,不答得1.5分,答错得0分,满分150分。
AMC10竞赛主要是针对10年级及以下学生,主要考察几何、数论、概率及统计、排列组合等部分的内容,但不涉及微积分,三角函数知识。有些问题的比较深奥的,像是一些逻辑推理题,都是需要花费时间思考的。
备考AMC10需要哪些基础?
备考AMC10需要掌握9-10年级的课内知识基础,特别是初等代数、基础几何学、初等数论、概率等问题。此外,学生需要了解数论、平面几何(多边形与圆)、立体几何、函数方程坐标系、排列组合与统计概率等重点知识。学生还需要记忆500+单词,以便更好地理解英文题目。如果学生能够在AMC8竞赛中获得18分或以上的成绩,那么可以去备考AMC10。
AMC10竞赛备考攻略
AMC10试题有难有易,但根据以往的试题正确率来看,想要取得一个高分并不是很容易的,那么如何备考刷题才能更加高效呢?
01. 总结经验
AMC10竞赛共25道选择题,考试时间只有75分钟,根据以往的考试情况来看,很多同学在规定时间内依旧不能做完试题,由此可见,答题速度和解题方法都是很重要的。
在刷题时,相同题型的解题方法可以做记录,不断刷题,不断更新该方法,获得更简单快捷的解题方法。通过自己总结的方法比任何人教授给你的都更适用!
02. 合理规划时间
AMC10试题从前到后试题难度基本是从简单到困难,需要考生在简单题上尽可能快速作答,能给难题留足作答时间。
AMC10后5道题比较难,对于想要冲刺前1%,5%的同学,建议同学们能够完全掌握1前20道试题,合理分配时间,给后5道题留足时间,争取争取一下更高的分数。
03. 分模块突破
在AMC10竞赛中,平面几何、数列、三角函数、概率等都有自身的突破技巧,比如概率要找题干中的关键词等等,这是需要大量刷题,并且老师指导历年真题趋势的情况下,才能达到的效果。
AMC10/12对比分析
AMC的进阶之路:
不管参加AMC10还是AMC12,都可以直接晋级AIME。一般中国孩子能在AIME中取得不错的成绩已经很有含金量。
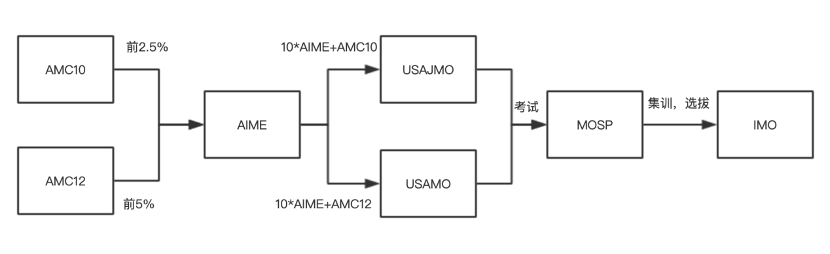

AMC10/12考点对比:
AMC没有任何官方的教材或辅导材料,对于考试也只给出了大概的要求,竞赛内容可以分为计数、数论、几何、代数、函数、复平面(AMC12独有内容)等几个模块。具体来说AMC10/12知识点主要有以下几部分。
1. AMC10考察范围
进阶代数:多项式,余数定理,韦达定理,根与系数的关系,特殊高次方程;进阶不等式、均值不等式;函数入门,定义域和值域、二次函数、指数函数、对比函数、简单三角函数;数列进阶;代数技巧进阶。
进阶几何:进阶几何作图;三角形进阶、正弦定理、余弦定理、内切圆和外切圆,斯图瓦尔特定理,共点和共线;圆和四边形,四点共圆,圆的外切四边形;正多边形,角度,周长和面积;进阶平面几何技巧;解析几何入门。
立体几何:点、线、面的关系,三维坐标系;立体几何作图;正多面体,欧拉公式;特殊的立体几何图形,立体几何技巧。
进阶数论:数,数组和序列;模运算,复杂同余问题;整数、分数和小数,进制转换;基本丢番图方程,进阶数论技巧。
进阶组合:容斥原理;二项式定理及相关结论;进阶排列、组合和概率;期望入门,递推、二分法,进阶组合方法。
2. AMC12考察范围
进阶代数:复杂不等式、调和不等式、轮换不等式、柯西不等式;复杂函数问题,反函数和符合函数,三角函数和差化积、积化和差,万能公式;复数,复平面,欧拉公式,蒂莫夫公式;数学归纳法、复杂数列和极限。
进阶几何:圆相关几何进阶;数形结合,二维、三维图形的函数表达,进阶解析几何;不规则二维、三维图形的处理;二维向量、三维向量。
进阶数论:二次余数,高次余数、费马圣诞节定理、费马小定理;各类丢番图方程的解法。
进阶组合:随机过程和期望;复杂组合问题技巧、基本综合问题。