今年的剑桥 STEP 2 考试已于上周落下帷幕,不少考生都反映此次试题难度不低,国际教育教研组老师第一时间对真题进行了分析。
本篇文章将由老师为大家解析 STEP 2 解题思路,希望能对后续的牛津 MAT备战有些启示!
总体点评:
今年这场STEP2考试结束后,听到最多的同学们的评价就是,计算量大,难度高,横向对比来看,这场考试难度比去年难度略高,相比于2020年难度略低。
23年STEP题型复盘,趋势精研
Q1 思路点评:
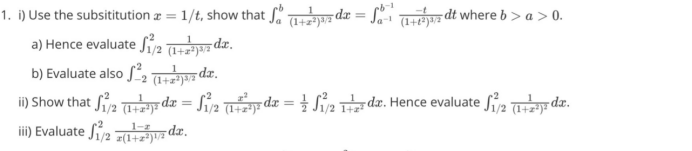
(题源于网络)
首先这道题作为开场第一题,一贯的属于官方想让大部分同学拿分的微积分类型。整体考察中规中矩,甚至比很多积分需要多次使用不同换元不一样,从头到尾使用的都是倒数换元。
而这种换元在许多年题目中都得到了应用,如2020-S2-Q1,2019-S3-Q5,2014S2-Q4,所以注重pastpapers刷题的同学开场应该比较顺利,题目第二部分和第三部分还使用到了积分的左右变换,均属于常规题型与难度。
Q2 思路点评:

这道题依然属于过往考察的高频考点三角函数。第一部分非常容易,涉及三角函数的倍角公式。值得注意的是,解决同名三角函数方程的时候,使用的是三角函数之间的角度周期变换,这种考察,在2017-S2-Q3,2015-S2-Q4,2011-S2-Q4都有所涉及。
在题目第一部分给了提示使用2倍角公式后,第二部分和第三部分分别拓展了3倍角公式以及余弦倍角公式。所以需要考生平时对三角函数的恒等式形式与常见的all solutions的写法要十分熟练。此外,第三部分涉及到了往常的重要考点——多项式方程根的范围,计算量稍大。
Q3 思路点评:

这道题的主旨是探讨和高次多项式求高阶导数,此类题型可以说非常常见了,比如1994-S2-Q2,2016-S2-Q3。特别值得提及的是本题出题人希望借由此题探讨一体多解,所以整体难度并不高。
可惜题目可能会因为貌似抽象,以及证明步骤多,很多同学不愿意选择。难度较高的是第二部分最后小问,出现了by parts 与reduction formulae结合的内容,在1998-S3-Q2,1991-S2-Q5,2021-S2-Q8,2013-S2-Q2都有过考察。对部分还没有学完高数知识点的同学可能存在障碍。
Q4 思路点评:

数列是近几年的考察重点,反复考察的内容包括数列的变化趋势、数列的极限、数列与不等式以及级数的结合等。这道题相比于前两年数列中需要大篇幅的逻辑证明(如2020-S2-Q3)不一样,主要是证明不等式,计算量不大。使用的主要方法和技巧与2009-S2-Q6那道Fibonacci数列的放缩法几乎一模一样。
Q5 思路点评:
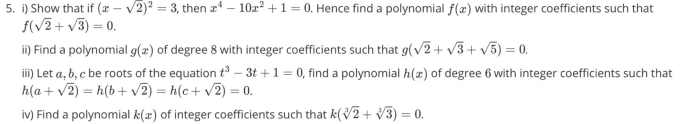
这道题考察的是最小多项式(minimal polynomial)。但是整体计算量十分惊人,特别是反复涉及到多项式的展开,建议同学们平时多手动展开或者记忆二项系数提升做题速度,整体来看应该是很多同学不愿意选择的题目,四个部分的思路依然是一脉相承,因此思维难度并不大。
Q6 思路点评:

近年来考察的超级大热门矩阵虽迟但到,而且依然出现在了偏后的位置。但是一如既往,难度不能算高。主要是考察矩阵的基本运算性质,矩阵的行列式性质,以及配合证明。
值得注意的是,2019年来几乎每年都有矩阵,几乎每年都是必考induction类型的证明题,而且与别的topic结合的考察法也是常规模式。今年结合的依然是大家熟悉的Fibonacci数列,以及二项展开级数的结合,二项级数是热门考点,大家如果平时积累过诸如1999-S2-Q4的做题经验,这道题应该可以拿下。
MAT备考
MAT学习建议:MAT的考试范围虽然不如 STEP那么广,但同样对考生在数学上的成熟度提出了很高的要求。立志成为 G5人的考生们,如果希望通过此次的 MAT敲开梦校大门,则需进入备战模式。
我们建议考生除了 MAT的真题练习外,在Alevel数学课程的学习过程中,不妨也提高一下对自己的要求。对教材中的原理和公式不再不求甚解,而是细究到底,真正搞懂所有的定理证明,对于给出的例题,不再满足于看懂过程,而是尝试用不同的方法去解答,对于各个模块零散的知识点,尝试用自己的理解去串连起来,慢慢建立起自己的知识体系。
如果能以如此态度学习数学,相信到了 MAT开考的时候,一定会有种脱胎换骨的感觉,不再害怕看似变幻莫测的考题。
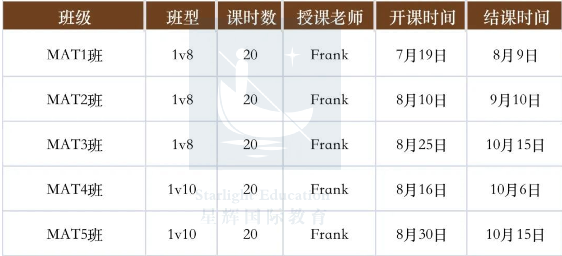
MAT笔试班课:
开课时间:7月~8月
上课时长:20课时