各位同学新年好,今天初三,春节继续给大家送福利,今天接着带来排列与组合、复数的讲解。
PART 1:排列和组合
在AMC中排列与组合考察的题目相对来说比较简单,主要通过以下方法进行求解:
① 常规的乘法原理、加法原理、排列与组合的混合运用;
②捆绑法、插空法等综合运用;
③排除法:at least, at most题型;
④分类讨论:不重不漏;
⑤重复排列、圆排列;
⑥伯努利分布、二项式定理、三项式定理或四项式定理的综合运用。
所以AMC在排列组合中难以出现比较困难的题目,只要以上知识点掌握熟练,然后注意细节,基本上还是不会出现特别困难的题目。但是在AIME题目中,以及比较困难的AMC题目,则从转化角度对排列组合这个知识点进行考察,基本上要把握好以下原则:
① 对文字语言转化为几何图形问题;
②把几何图形问题转化为方程组的解的问题,或者回到AMC所考察的知识点中来。
转化问题第I类:配对问题转化为几何图形问题
在AMC中曾经考察的类似题目为:
AMC 10-2012A-23

AMC 10-2012B-24

关于这两道题的解析,可以加后文的微信索取。AOPS的解析依然还是没有系统性的解决类似的的配对问题。
我们看一下AIME中的考察:

首先要理解这道题的题意,然后把这道文字题,转化为几何图形问题,就简单很多。
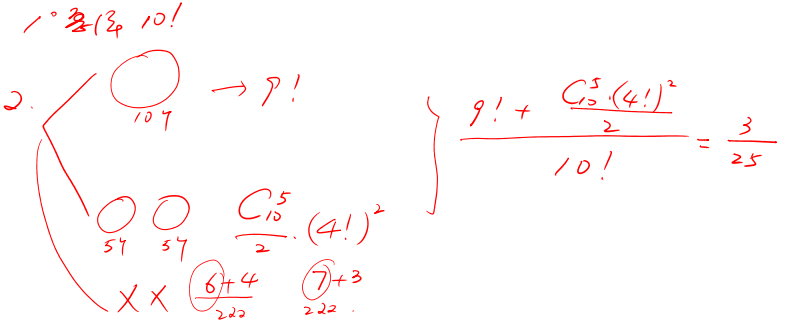
这道题很多同学疑问的地方是为什么10个围成一个圆圈符合、2个5+5的圆圈符合,而8+2,7+3,6+4的形式就不可以呢?因为注意到如果存在一个k使得条件不满足,则这个集合内部将实现一个置换。若使得不存在的置换,则只有两种情况,要么所有数是构成一整个置换,要么构成两个大小为5的置换,而8+2,7+3,6+4都可以找到一个相对称的置换。

当转化为几何图形时,分为四种情况,则题目就简单很多(注意:一共4种情况,容易漏其中一种或者两种):
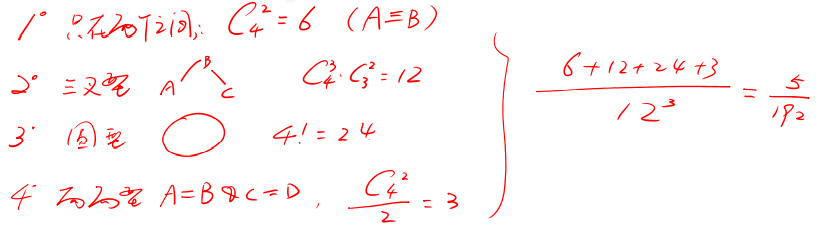
转化问题第II类:几何图形转化为方程组解的问题

下面同类型的题目就显得有点困难一些:

很多同学在处理这道题的时候,对减掉3*(50C2)不知道是什么原因导致的,这个题是经典的带限制条件的不定方程求组数解的题目。关于这个知识点,是AMC的知识点,我们简单再复习一下。
比如如下这两道题答案是不一样的:
①12x+4y+3z=567的非负整数解的组数;
②12x+4y+3z=567的正整数解的组数;
③12x+4y+3z=567且1≤x,y,z≤45的解的组数。
这个题目还是要用挡板法,用文字解释不清楚,语音比较方便,想要知道以上三个题目的区别,以及上文的“减掉3*(50C2)”的具体方法的,可以加我微信,然后语音和图片的方式来回复。有很多同学想要排除法,排除掉所有直角三角形和钝角三角形,也是可以的,就是略显麻烦。
我们再看一下在点拨(二)中提到的一道题:
![]()
上次我们是用代数的方法(具体可以看点拨二),现在我们用几何的方法再处理一遍:
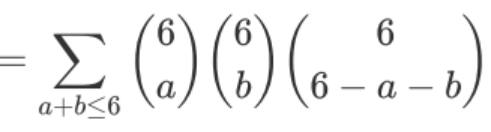
考虑3行6列的18个不同的小球,每次我可以选若干的点,总共选6个点。S是这样的选择的总个数,但我们也可以用下面的综合计数的方法:我从18个球中任意挑选6个,这两种答案应该是一样的。因此答案就是18C6=18564。
转化问题第Ⅲ类:分类与分步
分类讨论是所有竞赛都会考察的数学思想,需要掌握以下几点:
①不重不漏:这是最重要的;
②建立的分类标准,不能使分的类别超过5种;
③在分类时,对于一些复杂的题目,要把个例和通例结合在一起综合思考。
分步最关键的是分步的路径,一旦路径的顺序错误,将会非常麻烦,甚至会出现错误。
现实中很多题目,分类和分步是难以清晰的分开的,两者紧密的结合在一起。我们看一道题目,堪称是分类和分步在一起的绝好典型:

下面给出这道题的解析:
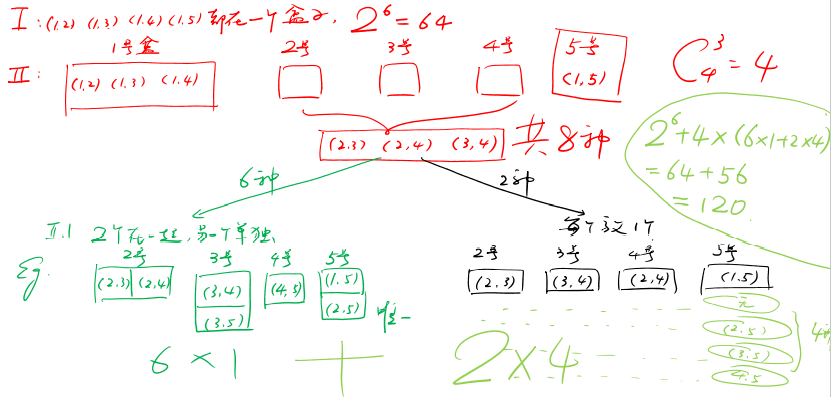
因为分类和分步是常规的题型,技巧性很传统,这里不再做进一步赘述。
Part II:复数
AMC比较喜欢考察复数的基础,比如高次方程的解的存在性、高次方程的解所围成的图形的面积,比如类似下面的题目:
![]()
所有的点所围成的凸面图形的面积;
或者
![]()
的四个点正好是一个椭圆焦点弦(过椭圆的焦点与长轴垂直的弦)与椭圆的四个焦点,求离心率e,等等,总体上来说,AMC对复数的考察还比较基础,难题集中在复数的高次方程的几何意义这个点上。
而AIME则要复杂一些,它着重于与多项式、数列、韦达定理、二项式定理等结合在一起考察,而且很容易出现高次项。比如如下的题目:
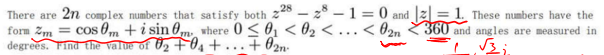
在具体解这个题目之前,我们看以下内容(w≠1):
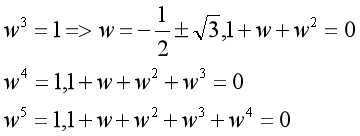
以上,很容易看出来|w|=1,推到的方式都是用的等比数列求和公式。
记住第一个公式,以及相应它的变形,因为以后你会经常用到。
以上题目经过变形为:
![]()
到这里之后,可以有多种处理方法,比如:
①两边同时取模,当然需要对
![]()
两边也要取模,然后联立求角度的值,想一下这是为什么?
②利用两边实部相等,虚部相等,然后列两个式子,求角度的值;
③采用猜的形式,这个最简单,就是z^8,z^28只能是
![]()
想一下为什么?
同样的,如下题:

很容易验证:
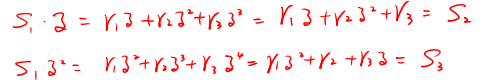
这证明了S1,S2和S3应该是x^3+C=0的三个跟,然后剩下的就很简单了,这是为什么呢?
这证明了S1,S2和S3应该是x^3+C=0的三个跟,然后剩下的就很简单了,这是为什么呢?