如何做对 STEP 2 每道题的最后一小问？

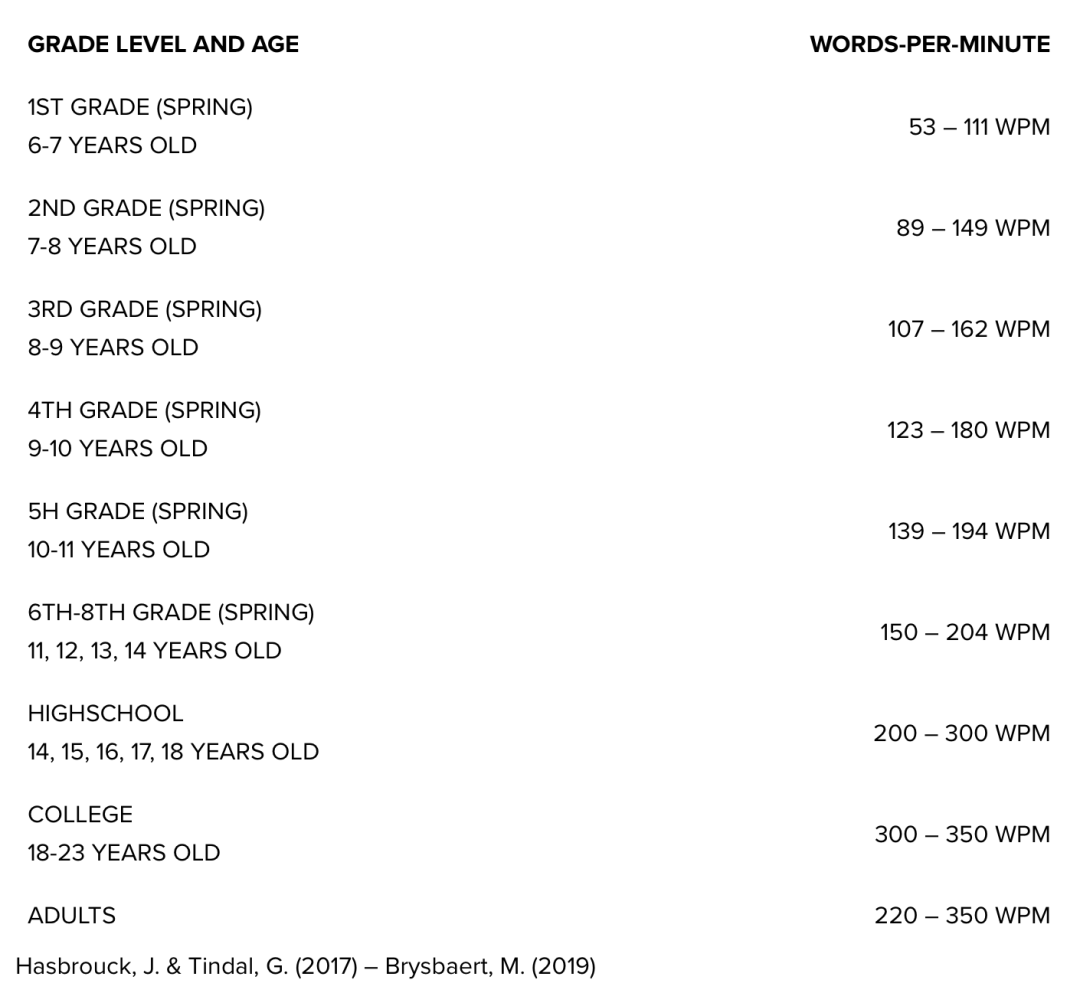
说起 STEP 入学考试，想必对英国留学有一定了解的学生和家长肯定听说过它。那么今天我们就来具体了解一下这项入学考试。

STEP（Sixth Term Examination Paper）考试是久负盛名的数学考试，考试目的是为了检测候选学生的数学能力。英国各大学会在给学生的预录取（Conditional Offer）里明确给出 STEP 考试成绩的要求。

该考试每年六月份在各个国家举行，由认证学校及考试中心组织考试，试卷统一寄回剑桥大学考试中心批改。STEP 考试共有三个等级：STEP 1、STEP 2、STEP 3。STEP 1 和 STEP 2 二者考查范围为 A-Level 课程所要求的大纲内容，而 STEP 3 的考查范围是 Further Math。

STEP 考试可谓是同学们踏入名校的最后一步，如何备考才能事半功倍，取得好成绩，实现名校梦呢？老师特意为同学们准备了详细的 STEP 2 考前指导，满满的干货，分享给所有有需要的同学！

很多同学进行 STEP 考试的时候，面临两个难点，一个是如何进行 8 选 6（我们假设选择纯数），第二个就是最后一问（一般来说第 3 小问）如何做，这样保证能够拿满分数。这两个的本质也是一个问题，就是尽可能的获得高分。

本文主要讨论第 3 小问的解法，因为一般来说第 1 问最简单，是考察基本功；第 2 问会稍微难一些，但是 A 或 A* 的同学经过努力，也是可以做出来的；第 3 问，则需要数学的技巧和能力，有竞赛功底的同学比较容易做得出来。我们通过一些例题来看一下。

第 I 类：第三小问带不等式类型

从某种程度上来说，不等式一种玄学，每一年高考，压轴题但凡出现不等式，基本上就是这一年的题目就会特别难，比如到目前为止高考题中最难的一道不等式题目：

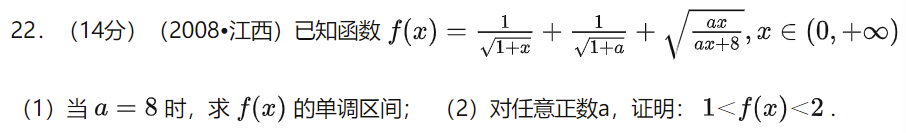
或者 1998 年全国高考一卷的数学证明题：

求证: m>n>3时，n^m>mⁿ

甚至是当年我高考的 2002 年，数学之所以没有拿满分，也是因为不等式

感兴趣的读者可以自行搜索这些题目的解析，我们会发现国内高考题的不等式的题目也是在最后一小问，而且这一小问，基本跟之前的小问关系不大。但是，对于 STEP 考试来说，是不是也是这样的关系的？

不是的，在 STEP 考试中，最后一小问，如果是个不等式，一定要使用之前的结论！

以下是 STEP 中相同类型的题目

其中第一小问，是一个简单的分部积分法，80% 的 STEP 2 的积分题目，如果你没有思路，勇敢的使用分部积分法即可。对于以下题目，肯定是使用分部积分法的：

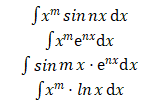
即不同类别的函数（幂、指、对、三角等）的乘积的形式要使用分部积分法；

第 1 问非常简单；第 2 问的证明，也是一个比较简单的证明；第 3 问的不等式则比较困难了。

比较复杂的第三个，其实是使用第 1 和第 2 的结论，然后进行简单操作即可获得。

我们也看一下第 3 小问，确实也是有难度的。

通过这道题，还是坚定一个信念，就是最后一小问，一定要利用之前的信息，进行处理。如果没思路，一定要勇敢的使用之前的第一小问和第二小问的信息。

第 II 类：不利用前面小问的结论，利用他们做题的逻辑

上面的这两道题特别有代表性，这类题型的特点是，前面比较简单的题目是“比着葫芦画瓢”，而最后一小问，则是“比着葫芦画勺子”，需要进行稍微创造性的解决问题。当然如果你的任课老师经历过国内的研究生入学考试（数一到数三），而且分数是在 140 分以上的话，那么他对这种类型的题目都是聊熟于心了，因为这都是基本功问题。

或者换一句话讲，你的 STEP 老师最好有研究生入学考试的经历而且获得了 140 分以上的分数，那么他对微积分这块会绝对掌握而且形成体系；如果他的高考数学分数是在 140 分以上，那么他对 STEP 中的初等数学这块，即三角函数、数列、函数最值、不等式、复数与向量使用等，也会绝对掌握且形成体系。

下面这道题是一个特别有意思的题目，第 1 小问和第 2 小问是在为你第 3 小问提供暗示，第 1 小问在告诉你如何选择 ≤ 部分，第 2 小问是在告诉你如何选择 ≥ 部分：

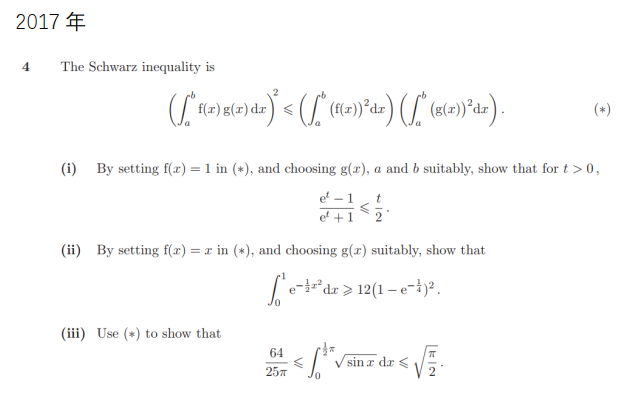
然而第 3 小问，不是简单的使用第 1 和 2 的结论，而是要复杂的多，因为没有告诉你选择什么样的函数，特别是 64/25π 会让很多同学抓狂，因为不好寻找具体的函数：

综上，我们介绍了高等数学部分的最后一小问做题的方法：一种是充分利用前面小问的结论；另外一种是充分利用前面一小问的方法。在下次的分享中，我们会介绍初等数学部分最后一小问做题的方法。