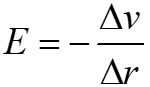数学建模的目的,在于抽象与简化复杂的现实世界,以及进行模型化,以便找到解决实际问题的方法。具体而言,数学建模的过程,是把问题转化为数学模型并求解的过程。在这一过程中,要根据实际问题、已知条件和数学模型(理论)之间的关系,建立数学模型并求解。
一般来说,数学建模需要掌握两个方面:一方面是学习各种基本数学知识和各种数学思想方法;另一方面是在实际应用中对这些知识和方法进行具体运用。在日常生活中,我们常常会遇到各种各样的问题,需要运用不同的方法来解决它,此时就需要有一个能够将这些方法应用到实际生活中去。
数学建模是在实际问题中提炼出一个能解决问题的数学模型,也就是将问题转化为数学模型。在这个过程中,我们就需要考虑该问题所用到的知识点、思想方法以及具体的数值计算过程等。
数学建模思想的核心是“化繁为简,以简驭繁”,即化复杂为简单。例如:在我们建立“最小二乘法”这个模型时,它并不是直接把最小二乘的结果作为目标函数来求解的,而是先利用最小二乘的方法求出最值后,再通过求解该问题得出在满足约束条件下应选择何种方法进行求解。
我们都知道,数学是人类思想的结晶,而数学建模是数学的重要应用之一。作为一名初高中学生,我们是否有过这样的困惑?为什么要去学习数学?我觉得这是一个很有趣的问题。作为一名高中生,我们有机会了解这个问题,去深入探索这个问题。我想在这里和大家分享一下我的一些思考。
首先,我认为学习数学就是为了更好地解决我们生活中的实际问题。我们可以看到在现实世界中,我们会遇到各种各样的问题,它们是由各种各样的因素(如:人、财、物)所影响,而且往往这些因素还不确定。由于人和事都是瞬息万变的,所以我们就很难去预测一些未来会发生的事情。例如:一架飞机在空中飞行时会遇到天气、地形等问题,这就需要我们考虑飞机是否能安全地降落、能否安全地通过一些地方等。
所以这就需要对未来进行预测。如果对未来进行预测的话,那就要考虑一些因素了——例如:飞机飞行时要考虑空气阻力、是否会受到天气影响等,因此在对未来进行预测时就要对这些因素进行研究和考虑了。上述例子中就涉及到了数学建模与预测的问题了——用数学建模去解决实际问题。当我们拿出一张纸和笔时,我们就可以把要研究的对象(人、财、物)和它们之间的关系记录下来,然后我们就可以用数学模型去解决它们了。
数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象,简化建立能近似刻画并"解决"实际问题的一种强有力的数学手段。数学建模就是用数学语言描述实际现象的过程。
这里的实际现象既包涵具体的自然现象比如自由落体现象,也包含抽象的现象比如顾客对某种商品所取的价值倾向。这里的描述不但包括外在形态,内在机制的描述,也包括预测,试验和解释实际现象等内容。我们也可以这样直观地理解这个概念:数学建模是一个让纯粹数学家(指只研究数学而不管数学在实际中的应用的数学家)变成物理学家,生物学家,经济学家甚至心理学家等等的过程。数学模型一般是实际事物的一种数学简化。它常常是以某种意义上接近实际事物的抽象形式存在的,但它和真实的事物有着本质的区别。
要描述一个实际现象可以有很多种方式,比如录音,录像,比喻,传言等等。为了使描述更具科学性,逻辑性,客观性和可重复性,人们采用一种普遍认为比较严格的语言来描述各种现象,这种语言就是数学。使用数学语言描述的事物就称为数学模型。有时候我们需要做一些实验,但这些实验往往用抽象出来了的数学模型作为实际物体的代替而进行相应的实验,实验本身也是实际操作的一种理论替代。
此外,数学建模是在20世纪60和70年代进入一些西方国家大学的,中国的几所大学也在80年代初将数学建模引入课堂。经过20多年的发展,绝大多数本科院校和许多专科学校都开设了各种形式的数学建模课程和讲座,为培养学生利用数学方法分析、解决实际问题的能力开辟了一条有效的途径。
数学建模与我们日常生活息息相关,世界需要数学建模。