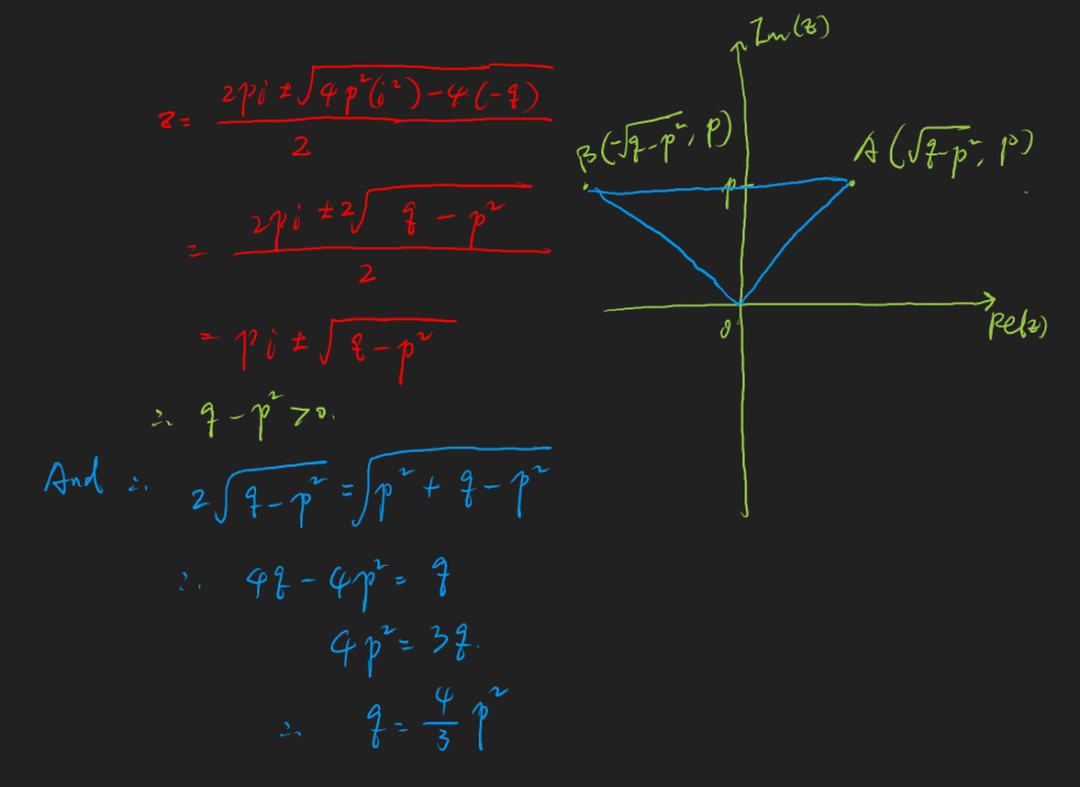2021数学P3复数题目详解

今天我们来解析一道P3的复数方面的题目。

虽然每年的考试题目都有一定的类似之处，但是有些题目的出题的角度和考察的内容是和其他同章节的题目有一定的不太一样的，同学们在遇到这一类的问题的时候往往会觉得这些题目比较怪异，那么今天我们来看一下这道复数的题目怪在哪里。

这道题目选自2021年春季编号31的卷子，原题如下：

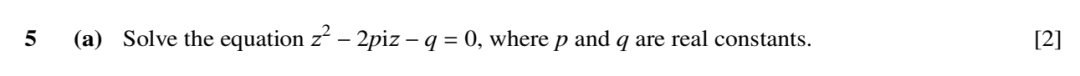
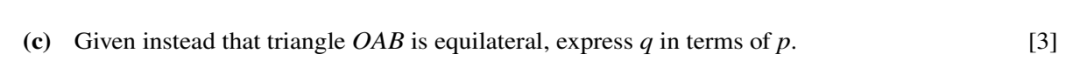
（a）问是解方程，我们只能用二次方程的求根公式来求，解题过程如下：

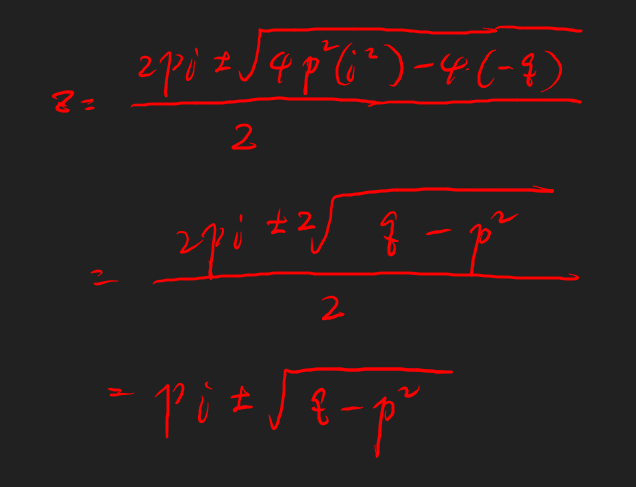
（b）问是说在argand 图中，上述方程的2个根代表两个不同的点A,B，而且A,B两点都在虚轴上，求p和q之间的关系。

请注意，两个不同的点是关键，很多同学这道题之所以出错就是在这里，没有理解什么叫做2个不同的点。

我们来分析一下，首先，pi是相同的，所以如果根号里面的那个式子等于0的话，那么AB两点便相同了；第二，如果根号里面的式子大于0的话，那么AB两点的实数部分必然一正一负，那么就不可能落在虚轴上了；所以，根号里面的式子必然小于0，解题过程如下：

c问是说OAB这三点形成等边三角形，此时AB两点还是不同的两点但是不同在虚轴上了，因为如果AB这两点还是在虚轴上的话OAB三点在一条直线上不可能形成三角形。解题过程如下：