求交集或并集是集合的两种特别重要的运算。很多时候我们需要知道多个集合的并集的元素个数,或者更一般的说法叫测度,然而实际上更容易直接获取的是集合之间的交集的测度。幸运的是容斥原理(Principle of Inclusion-Exclusion)可以将多个集合之间的并集的测度用交集的测度和集合各自的测度表示出来。因此,容斥原理在组合数学、概率论与数理统计中有重要的应用。
容斥原理
在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
换言之,容斥原理就是:
1. 容:先把所有对象都先加起来
2. 斥:仔细想想哪些对象算重复了?重复计算几次?
3. 定量地斥:计算1次的对象保留,计算2次的对象要减去1次,计算3次的要减去2次,这样就保证了每个对象的数目都被计算了1次,从而保证了不重不漏。
通常使用容斥原理可以计算两个或者多个不同的类别重叠部分元素的个数。它的集合表达式如下,一般来说只需要掌握两集合,三集合对应的结论就可以了。
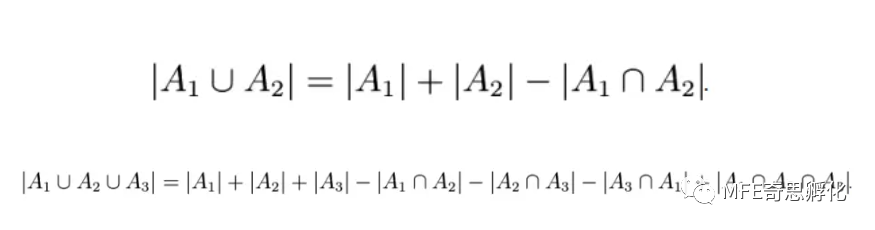
如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。(A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C)。
例如:一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?
分析:依题意,被计数的事物有语、数得满分两类,“数学得满分”称为“A类元素”,“语文得满分”称为“B类元素”,“语、数都是满分”称为“既是A类又是B类的元素”,“至少有一门得满分的同学”称为“A类和B类元素个数”的总和。为15+12-4=23。
在几何方面,容斥原理的几何意义可以理解为:平面上两个几何体覆盖区域的面积等于它们各自的面积之和再减去相交区域的面积;三个几何体覆盖区域的面积等于三者各自的面积之和减去两两相交区域的总面积,再加上三者相交区域的面积。事实上,这正是表示集合之间关系的韦恩图的思想。
根据容斥原理可以推导出复合事件的概率公式。比如对于两个事件A、B,记各自发生的概率分别为P(A)和P(B),同时发生的概率为P(A·B),至少有一个发生的概率为P(A+B),那么
P(A+B)=P(A)+P(B)-P(A·B)
跟集合的容斥原理的形式是一样的。对于更多事件组成的复杂事件,其概率公式也可以类比集合的容斥原理公式得到。事实上概率本身就是一种测度。
在容斥原理公式的右边各交集前面的符号随求交集的元素的个数的增加而交替地变化,实际上就是在反复执行“多退少补”的操作。
这个知识点在2021年AIME II 第六题中被考察的就是容斥定理的应用。