AMC不同于其他的数学比赛，它的体系环环相扣，颇有打怪升级的感觉。
对于中国学生来说，AMC 8/10/12，包括之后的AIME都是可以参加的，但再往上的USAMO则是为了选拔美国奥数国家队队员设立的，相当于我们国内的“国家集训队”，只有美国公民或美国/加拿大的合法居民可以参加。
而对于名校申请，特别是MIT、斯坦福、普林斯顿，光从AMC晋级AIME还不够，如果AIME成绩要达到晋级USAMO的成绩，则更有优势，因为每年晋级USAMO的学生人数不超过300人，是当年全美乃至全北美洲数学最强的学生，极其受到藤校的青睐。
随着参赛人数逐年增加，想在AMC中胜出越来越难，我们也为大家准备了AMC四大题型及解题秘笈。
AMC四大题型及解题秘笈
题型二：几何题
几何一词源于《几何原本》的翻译。徐光启和利玛窦翻译的时候，取原文“geometria”的第一个音节“geo”的音译为“几”，而“几何”本身在中文里是“衡量大小”的意思，用“几何”来作为中文译名，音义兼顾，是神来之笔。
几何学从诞生开始，就是衡量图形的大小的一门数学分支。几何的能力，就是如何将我们视觉看到的一维（长度）、二维（面积）和三维（体积）的图形进行数量化的能力。在视觉的图形关系中，去探索数量的比例关系，图形中寻找“几何”，这就是这种题型的精髓。
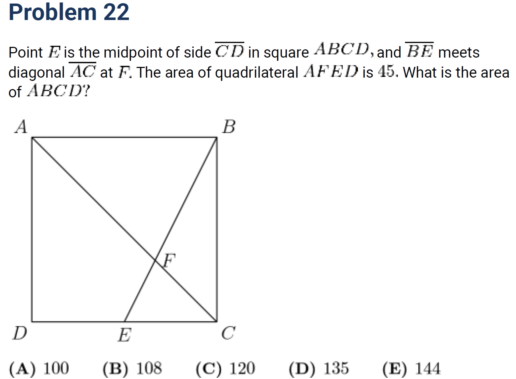
2018年AMC8 第22题。2018年题是近10年来最难的一套。
解题思路：从图形上来看，一个正方形被两条直线分割成了4块，所以关键是这4块面积之间的比例关系，或者说它们分别占到整个正方形面积的几分之几。我们注意到其中3块都是三角形，而且只要知道这3个三角形的面积比例，不规则四边形AFED也就知道了。三角形面积比例常用到的几种方法：1）相似三角形面积比是边长比的平方；2）同高三角形的面积比是底边之比；3）同底三角形的面积比是高之比。
学生需要培养“维度”的概念。二维的数量大小是一维的平方的关系，三维的数量大小是一维的立方的关系。而在科幻小说《三体》中，质子是处于卷缩状态，被N维展开以后就会达到N次方那么大，就是非常大的数了。只有在直观范围内把数量关系理解好，将来才能向远远更抽象的高等数学发展。数学实际是纯抽象的学科，数学概念只要能定义就存在，并不需要对应到现实的实物。
【竞赛报名/项目咨询+微信：mollywei007】
