2024-2025年度的USACO竞赛12月赛季已经落下帷幕,机构也收到了不少同学晋级的喜讯,有从铜级直升金级的大神级选手,也有非满分晋级1月赛季继续冲击奖项的同学。那么在USACO计算机竞赛中能更好地帮助我们解决复杂问题的“深度优先搜索”究竟应该如何应用呢?
在USACO(美国计算机奥林匹克竞赛)中,深度优先搜索(DFS)是解决许多复杂问题的关键工具。今天,我们一起来探索DFS在USACO中的应用及其技巧!
什么是DFS?
在学习铜牌阶段内容时,大家在USACO Guide中会发现一个名为Complete Search(完全搜索)的章节,在该部分,我们通常都会引入一个N皇后问题来带领大家了解全排列的思想,但是很多同学在学习N皇后问题的时候基本都是一知半解,对于代码的逻辑并不能深入了解。实际上N皇后问题的实现借助的就是DFS的思想。
DFS是一种用于遍历或搜索图和树的算法。它沿着每条可能的分支尽可能深入地搜索,直到无法继续为止,然后回溯到上一个节点继续搜索其他分支。在N皇后问题中,我们便是采用了DFS的思想,放置一个皇后之后,会在下一行进行尝试,如果下一行所有的位置均不能放置,那么会回溯到上一行,将上一行的皇后重新进行放置。继续尝试下一行的放置,如果无法放置,则会回溯到上一步重新进行尝试。
DFS遍历过程
以Tree(树)数据结构为例,我们来深入理解一下DFS的应用流程:
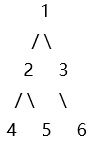
上图是一个树,节点1是根节点。节点1连接到节点2和节点3。节点2连接到节点4和节点5。节点3连接到节点6。DFS的基本思想是尽可能深地探索每一个分支。
当遇到一个节点时,首先访问该节点的一个未被访问的子节点,直到没有未被访问的子节点为止,然后回溯。对于上述树结构,DFS的遍历顺序如下:
1. 访问节点1(根节点)
2. 访问节点2(从节点1开始,选择左子节点)
3. 访问节点4(从节点2开始,选择左子节点)
4. 回溯到节点2
5. 访问节点5(从节点2开始,选择右子节点)
6. 回溯到节点2,再回溯到节点1
7. 访问节点3(从节点1开始,选择右子节点)
8. 访问节点6(从节点3开始,选择右子节点)
完成遍历
DFS的代码实现
DFS通常通过递归函数实现,代码简洁直观,以下是一个在图中使用DFS访问每一个节点的代码,备考时可以以该代码为基础框架,进行改进和优化。
DFS在USACO中的常见应用
1. 连通性检查
- 判断图中是否所有节点都连通。
- 识别独立的子图,帮助解决分组或连接问题。
2. 环检测
- 识别图中的环路,常用于检测冗余连接或避免重复路径。
3. 路径寻找
- 在迷宫或网格中找到从起点到终点的路径。
- 计算路径的数量或最短路径。(Gold)
真题演示
我们以2019年3月铜牌第三题为例,题目如下:
题目背景:在3019年,牛类经历了显著的进化,发展出各种有趣的特征。这些进化过程可以用一棵树来描述。
树的结构:
根节点:代表最初的祖先牛,没有任何特殊特征。
内部节点:每个节点代表一次进化事件,可以是所有后代牛获得一个新特征,或者是分裂出部分后代获得新特征,部分不获得。
叶节点:代表最终的牛的子群体,每个叶节点的特征组合都是独一无二的。
“Proper”进化树的定义:一个“proper”的进化树满足以下条件:每个新特征只在树中的一条边上出现一次。也就是说,每个特征都是在树的某个特定的进化步骤中产生的,而不会在多个独立的进化路径中独立出现。
任务:给定若干牛的子群体及其特征组合,判断是否存在一棵“proper”的进化树能够解释这些子群体的特征组合。
使用DFS思想解决问题
1. 收集所有特征
首先,收集所有子群体中的特征,建立特征的集合。
2. 构建特征依赖图
初始化:
- 将所有特征作为图的节点。
- 创建一个邻接表来表示依赖关系。
确定依赖关系:
- 对于每个子群体,比较其特征与其他子群体的特征,找出可能的进化路径。
- 如果某个特征只在特定的子群体中出现,则可以推断它的进化步骤。
3. 检测环路
- 使用DFS遍历图,检测是否存在环路。
- 如果存在环路,说明某些特征存在多重进化路径,不满足“proper”进化树的要求。
4. 拓扑排序
- 如果图中没有环路,可以进行拓扑排序,确定特征的进化顺序。
- 拓扑排序确保所有特征的进化顺序是线性的,没有冲突。
5. 判断结果
- 如果图中没有环路且拓扑排序成功,输出"yes"。
- 否则,输出"no"。
DFS学习建议
以上是DFS的讲解,随着近些年难度的增加,铜牌阶段的题目也可以采用DFS算法来解题,因此DFS的考察范围贯穿所有段位。提升DFS的方式是多练习,真题通常体量比较大,在初期阶段,大家可以在leetcode中练习DFS中的简单题目,从简单题目入手,逐步过渡到USACO中的真题。