新加坡数学为什么能常年排名全球前列？

在构思这篇文章时，我一想到我的学生们解数学题的场景，脑海中就不自觉蹦出了一堆表情包。

在数学学习中，题型的丰富性既带来了挑战，也带来了乐趣。从选择题到填空题，从计算题到作图题，再到文字应用题，每一种题型都有其独特的特点和要求。

然而，当被问到哪种题型最让人头疼时，不妨大胆猜测一下，选择“文字应用题最难”的人，人数恐怕会“一骑绝尘”。

这就引出了一个有趣的问题：文字应用题真的有这么难吗？

大多数学生在面对文字应用题时，通常会采取以下五个解题步骤：

1️⃣ 完整读题

2️⃣ 开始解题

3️⃣ 解题过程中遇到卡壳的地方，重新读题

4️⃣ 代入数据时，再返回题目中寻找

5️⃣ 最后完成解答

这「五步走」看起来逻辑清晰，似乎没什么问题。然而，仔细分析会发现，这样的解题步骤其实存在不少隐患，尤其在考试这种时间紧张的场景下，效率和效果可能会大打折扣。为什么这么说呢？原因可以归纳为以下三点：

1. 费时

文字应用题往往题干较长，信息量大。当你第一次完整读题时，大脑需要花费较多时间去处理和整合这些信息，以建立起清晰的逻辑链条。

然而，如果在解题过程中遇到“卡壳”，又需要返回题目重新阅读、重新理解，这种反复的过程无形中浪费了大量时间，导致解题效率大幅下降。

在考试中，时间分配至关重要。如果每道文字应用题都耗时过多，不仅会降低整体解题速度，还会影响对其他题目的完成情况。

2. 费力

文字应用题的题干通常包含大量条件和数据，有时甚至隐藏了多层逻辑关系。学生在面对这些复杂的信息时，需要不断筛选、提取和归纳，整个过程对大脑的处理能力提出了极高要求。如果缺乏技巧，甚至连解题的切入点都难以找到，这种情况下，学生往往会感到非常吃力，产生心理负担。

特别是在面对冗长的题目时，光是把题目读懂、条件整理清楚，就已经耗费了大量脑力，导致后续解题时显得力不从心。

3. 完成度两极化

文字应用题的解题过程高度依赖逻辑链条的完整性，一旦某个环节出错，就可能导致整道题无法完成。在考试中，如果每道题都需要高强度的思考和逻辑推演，大脑“短路”几乎是不可避免的现象。

这种情况下，文字应用题的完成度往往呈现两极化：要么思路清晰、步骤完整，得出正确答案并拿满分；要么因为某个环节出错或逻辑不通，导致整题不得分。这种极端的分数表现，既影响了考试的整体成绩，也容易让学生在心理上产生挫败感。

那么正确且高效的解题方法有没有呢？

这就不得不说下新加坡数学了，他们的数学成绩常年在国际上都是排名第一的，而保持如此好成绩的他们，采用的数学方法也是备受国际好评——数学建模。

我带大家来切身感受下数学建模法对解文字应用题有什么帮助！

例题：

解题过程：

我们先来看一下第一句话：There were 3/4 as many sweets in box A as in box B.。

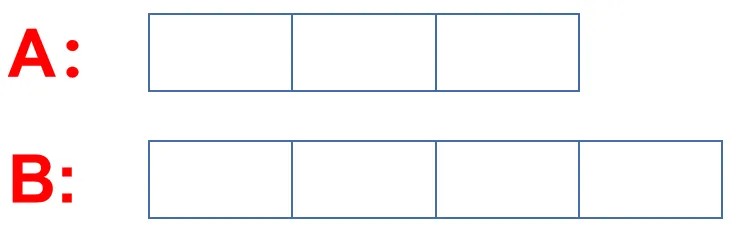
因为题目说 A 是 B 的 3/4 ，那我其实就可以给A先画 3 个相同的小方块，B画 4 个相同的小方块，这样就能很直观的体现出 3/4 的关系。根据这句话我们其实就可以画出如下图，

我们再来看一下第二句话：1/2 of the sweets in box A and 3/8 of the sweets in box B were removed. 。

这句话说盒子 A 扔掉了1/2，盒子 B 扔掉了 3/8，那我们是不是可以理解为盒子 A 扔掉了一半，而盒子B把自己分成 8 块且扔掉了其中 3 块。

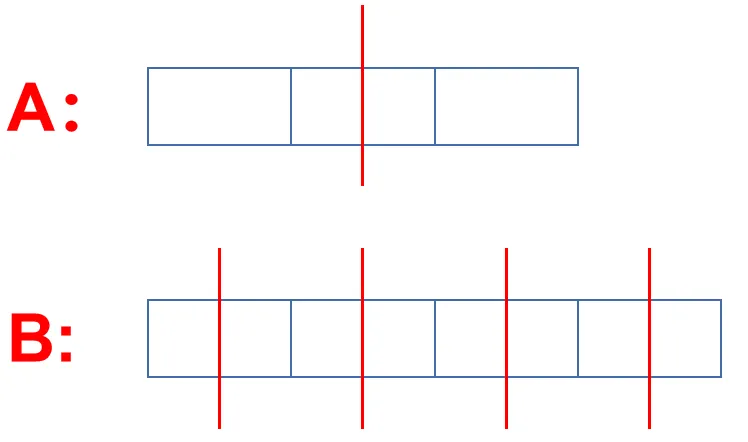
那么盒子 A 的 3 块方格，切掉一半是不是就如下图，而 B 只有 4 块方格，那是不是必须首先先把自己切成 8 块方格，这样才方便我们数格子，所以就如下图：

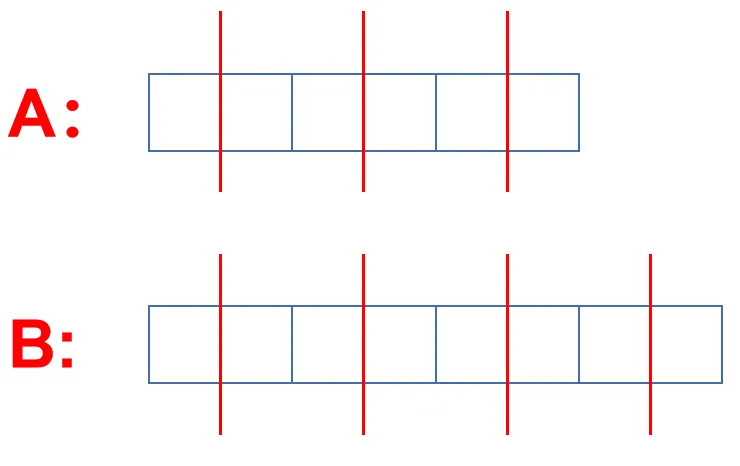
这样你会发现格子的大小不一，那为了保证我们的格子都一样大，我们就可以对盒子 A 的剩下 2 个方格进行平分，就如下图：

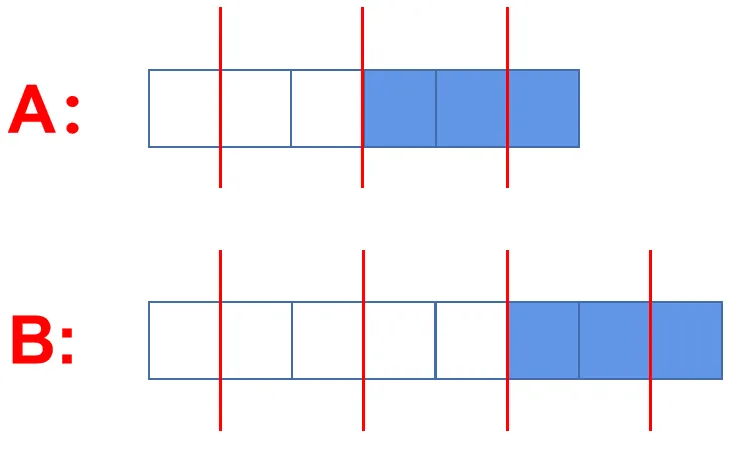
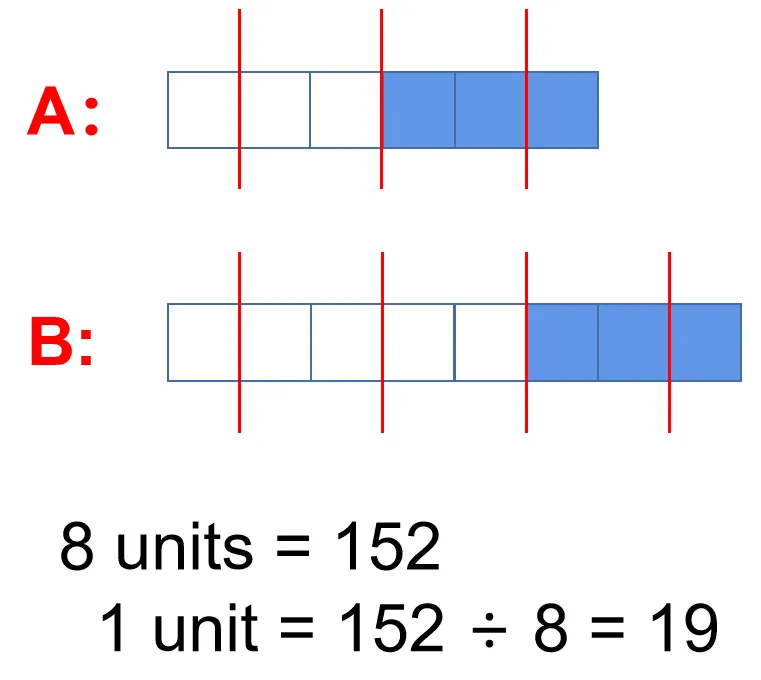
而第二句话需要我们把盒子 A 扔掉了 1/2，盒子 B 扔掉了 3/8，涂蓝色代表舍弃，白色代表剩余，所以就变成了下图：

我们接下来看一下第三句话：There were then 152 sweets left in both boxes altogether 。

这句话说他们总共剩下 152 颗糖果，我们对照上面这幅图，就可以得到 8 个这样的小方块就代表 152 颗糖果。所以计算过程如下：

我们来看下题目要求：How many sweets were there in each box at first?，问的是原先盒子中各有多少个糖果。

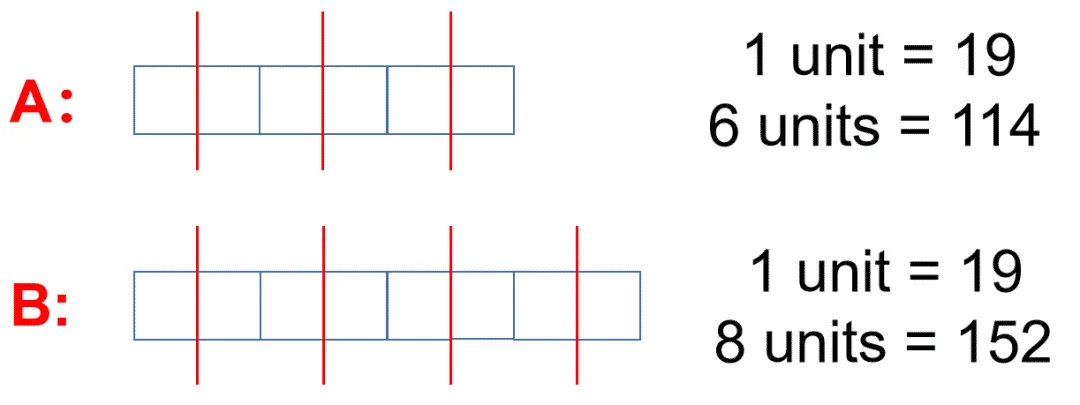
我们现在知道一个小方块代表 19 颗糖果，所以我们就能依次得出盒子 A 和 B 原来的数量，如下图：

最终我们得出盒子 A 原来有 114 颗糖果，盒子 B 原来有 152 颗糖果。

以上便是数学建模法的解题思路。大家会发现以下 3 点有趣的现象：

将题目的信息量都转化成图形的形式来表达；

不需要完整读完题才能解题，甚至可以将题目拆分成一句一句来解题。

边读题边画图，把题目读完了，答案也就出来了。

数学建模法打破了学生审题困难和解题困难的窘境，且能够让学生系统性的建立起数感和知识框架，这便是新加坡学生的数学锦囊。

所以，数学能力强的同学，可以好好掌握数学建模法。

这会让你的数学成绩和能力更上一层楼；数学能力不好的同学，更需要着重掌握数学建模法，因为这是让你数学成绩提升的最有效方法。