国际学校从小学 PYP 阶段进阶到 MYP 中学阶段,我个人觉得逆推能力的培养必须放在首位。不夸张地说,有了这个能力能让你省将近 50% 学习时间。
什么是逆推能力?举个简单的例子,大家或多或少都接触过锻炼思维的迷宫趣图,那么一般来说,如何最快找出从入口到出口的线路呢,相信很多人和我一样,都是从出口倒着画到入口的。
那么所谓的“逆推”能力在初中数学中又是怎么实现的呢。这里就不得不提及整个初中数学学习中最重要的知识点之一:因式分解 (factorization)。
很多初次学习因式分解的孩子们都称它为初中代数的“梦魇”。简单的说因式分解本身就是在代数式展开(algebraic expansion)基础上的逆运算。在我们开始学习代数时,首先掌握的是代数式的四则运算。这其中练习比较多的就是乘法分配律,例如这样一个式子:
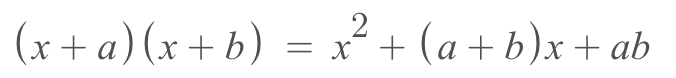
紧接着,因式分解就登场了!还是同样一个等式,原来是从左到右,现在要求我们从右到左计算:
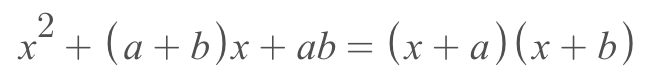
乍一看,好像没什么区别。但是当题目变成具体的数字的时候,尤其是数字稍微大一点,很多同学就“抓瞎”了。其实思路很简单,只需要逆向去思考,哪两个数字相乘等于 48,相加等于 14 就可以了。实际计算中,我们更侧重于找到相乘等于 48 的数字组合,也就是 48 的因数们。
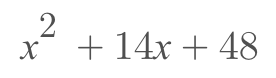
如果平方项的系数也变成一个可以因数分解的数字,怎么办呢?例如要对下面这个式子进行因式分解:
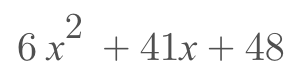
只需要多做一次逆向推导就好了,2x 乘以 3x 才会得到 6x², 所以两个括号中 x 的系数分别为 2 和 3。因为 48 的因数比较多,所以我们需要一对对的去验证或者使用十字相乘法。本质上,等同于进行了第二次的逆推导运算。

这里可能有同学会有这样的疑问,是否需要把常数项所有的因数配对都试过一遍呢?我的回答是,不需要全部都计算一遍。找出配对的快速方法其实就是通过不断练习,能够反应出大部分常用数字的因数配对,同时估算中间项 x 的系数是否接近给出的数字。
训练时间的加成,会让因式分解的准确率和速度不断提升。对于数学而言,最好的提升思维训练的方法:针对知识点做足量的练习,练成本能一般反应迅速。









