AMC10(American Mathematics Competitions 10)是美国数学协会主办的一项面向中学生的数学竞赛,旨在激发学生对数学的兴趣并提高他们的数学能力。本文将详细介绍AMC10考试中常见的题目类型,帮助考生更好地理解和准备这项重要的竞赛。内容包括:1. 基础代数题型;2. 几何题型;3. 数论题型;4. 组合与排列题型;5. 应用题型;6. 图形与图表分析;7. 常见问题解答。通过这些内容,读者将能够全面了解AMC10考试的题目类型及其特点,从而制定出更有效的备考策略。
一、基础代数题型
基础代数是AMC10考试中最常见的一类题目,这类问题通常涉及变量、方程以及函数等概念。在这一部分,考生需要掌握基本的代数运算,包括加减乘除、因式分解和求解方程等。以下是一些典型的问题类型:
线性方程:这类问题通常要求考生解一元一次方程或二元一次方程组。例如,给定一个简单的线性方程 (2x + 3 = 11),考生需要找到 (x) 的值。
代数表达式简化:这类问题要求考生对复杂的代数表达式进行化简,如合并同类项或因式分解。例如,将 (x^2 + 5x + 6) 化简为 ((x + 2)(x + 3))。
不等式求解:在某些情况下,考生还需解决不等式,例如 (3x - 2 < x + 4),并找出满足条件的所有整数解。
基础代数题目的关键在于熟悉各种运算规则,并能灵活运用这些规则解决实际问题。
二、几何题型
几何部分是AMC10的重要组成部分,其内容涵盖平面几何和立体几何。这些问题通常涉及图形特征、面积计算、周长以及角度关系等。以下是几种常见几何题型:
三角形和四边形:许多几何问题会涉及到计算三角形或四边形的面积与周长。例如,给定一个底边为5,高为12的直角三角形,需要计算其面积。
圆:关于圆的问题也相当普遍,包括圆周长、面积及弦、切线等相关性质。例如,如果半径为7,则圆的面积可以通过公式 (A = \pi r^2) 来计算。
相似与全等:这类问题要求考生利用相似三角形或全等三角形之间的关系来解决实际问题,比如求出未知边长或角度。
在准备几何部分时,熟悉各种公式及其推导过程非常重要,这样才能快速准确地解决相关问题。
三、数论题型
数论部分主要关注整数及其性质,包括因子、倍数和质数等。这些问题往往需要较强的逻辑思维能力和一定程度上的创造力。以下是一些典型的问题类型:
质因数分解:许多数论问题会要求考生对一个整数进行质因数分解,例如将30分解为 (2 \times 3 \times 5)。
最大公约数与最小公倍数:这类问题通常要求找出两个或多个整数之间的最大公约数(GCD)或最小公倍数(LCM),例如求12和15之间的GCD。
模运算:模运算也是AMC10中的一部分,例如计算某个数字除以另一个数字后的余数,这在解决某些特定类型的问题时尤其有用。
掌握基本的数字性质及相关定理,可以帮助考生在面对复杂数字时迅速找到解决方案。
四、组合与排列题型
组合与排列主要研究如何从一组对象中选择子集,以及这些对象如何排列。这一部分通常涉及计量方法,如排列组合公式。在AMC10考试中,这类问题一般具有较高难度,但也极具挑战性。以下是几个主要方面:
排列计算:例如,一个班级有5名学生,要安排他们站成一排,有多少种不同的方法?这个可以使用阶乘来计算,即 (5!)。
组合选择:如果班级里有8名学生,要从中选出3名参加比赛,有多少种选择方式?这个可以使用组合公式,即 (\binom{n}{r} = \frac{n!}{r!(n-r)!})。
应用场景分析:一些复杂的问题可能结合了以上两种情况,例如同时考虑选拔和排序,这就需要综合应用上述知识点来得出结果。
对于组合与排列的问题,多做练习能够帮助提升应试能力,并能更好地理解计量方法背后的逻辑。
五、应用题型
应用题是一种将数学理论应用于实际情境中的问题。这些题目通常结合了多个数学领域,如代数、几何和数据分析。在AMC10中,应用题不仅测试学生对知识点理解,还注重逻辑推理能力。以下是一些常见形式:
日常生活中的情境:例如,一个商店卖出的商品打折后价格是多少?这种情况下,需要设定变量并建立方程进行求解。
速率与时间关系:如火车行驶速度为每小时60公里,它行驶120公里需要多少时间?此时可使用速率=距离/时间公式进行推导。
投资与收益分析:如某人投资1000元,每年获得5%的利息,那么经过几年后总金额是多少?这种情况可利用复利公式进行计算。
掌握应用类型的问题能够帮助学生学以致用,提高他们对现实生活中数学知识运用能力,同时增强应试信心。
六、图形与图表分析
随着数据素养的重要性不断上升,在AMC10考试中也逐渐加入了图形与图表分析这一部分。这类问题要求考生能够从图表信息中提取关键信息并作出合理判断。以下是几个方面:
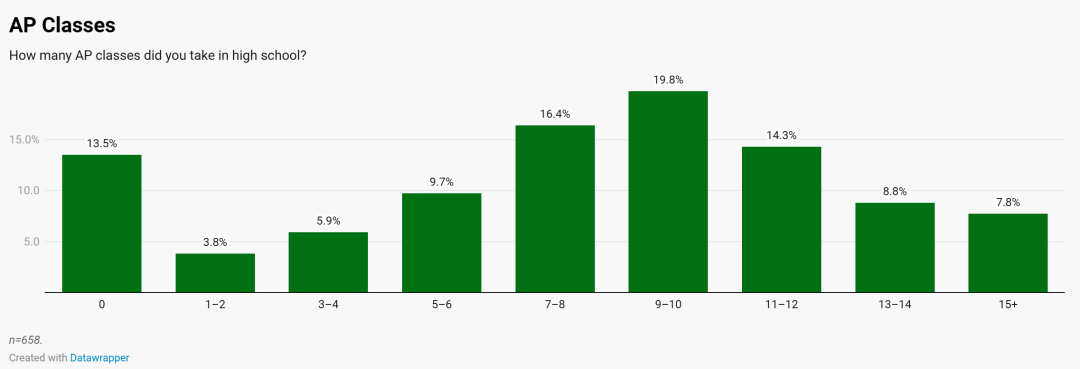
条形图和饼图解析:例如,从给定饼图中判断各个类别所占比例,并回答相关统计数据。
折线图趋势分析:通过观察折线图变化趋势,可以预测未来发展方向或者总结过去的数据变化情况。
数据总结报告撰写: 在某些情况下,需要根据提供的数据撰写总结报告,以便清晰呈现结果和结论。
具备良好的数据处理能力不仅能提高应试技巧,也能让学生在未来学习生活中受益匪浅。
七、常见问题板块
AMC10考试难度如何?
AMC10考试被认为是一项适合初高中阶段学生参与的重要赛事,其难度适合大多数具有一定数学基础且热爱学习数学的人群。不过,对于不同水平层次的人来说,其挑战程度可能存在差异。因此,建议参与者提前做好充分准备,以便顺利应对各种难度的问题。
如何有效备战AMC10?
备战AMC10可以采取多种方法,包括系统复习教材知识点、多做历年真题以及参加模拟测验。此外,与同伴一起讨论疑难杂症也是一种很好的学习方式,通过交流能够加深理解,提高解决复杂问题的能力。同时,不要忽视心理调节,在临近考试时保持良好的心态尤为重要。
是否需要报辅导班参加培训?
报辅导班是否必要取决于个人情况。如果自学能力较强且已有一定基础,可以选择自主学习,通过网络资源、自习室材料来备战。但若自我感觉薄弱或者缺乏系统性的学习计划,则报辅导班可能会更有帮助。在选择辅导班时,应注意教员资质以及课程安排,以确保获得高质量教育资源。