截至北京时间本周二晚,USACO 本赛季第一场12月晋级赛正式结束, 满分同学会当场晋级,没有当场晋级的同学可以耐心等待一周之内出成绩。
2024-2025年USACO计算机竞赛12月赛题出炉!让我们一起来了解一下吧
USACO 2024 DECEMBER CONTEST
BRONZE(铜级)
第一题

题目描述:
奶牛贝茜正在上学!她在做数学作业,其中她需要将正整数四舍五入到 10 的幂次。
将一个正整数a 舍入到离其最近的10**b,其中b 是正整数,贝茜会按照以下步骤操作:
1. 找到从右侧数的第 b 位数字。记这个数字为 x。
2. 如果 x≥5,贝茜会将 10**b 加到 a上。
3. 然后,将 a 的所有低于第 b 位(包括第 b 位)的数字设为 0。
例如:
* 如果贝茜想把 456 四舍五入到最近的10**2(即百位),她会找到第 2 位数字是 5(x=5),因此会加上 100。最终结果是 500。
* 如果贝茜将 446 四舍五入到最近的 10**2,她会得到 400。
在观察了贝茜的作业后,埃尔茜提出了一种新型的舍入方法:连锁舍入。对于连锁舍入到最近的10**b,埃尔茜会依次按以下顺序操作:
1. 先舍入到最近的 10**1,
2. 然后舍入到最近的 10**2,
3. 依次类推,直到舍入到最近的 10**b。
贝茜认为埃尔茜的做法是错误的,但因为忙于数学作业,她希望你帮忙确认以下问题(任务):
计算至少为 2 且至多为N 的整数x 的个数,使得:
* 将 x 舍入到最近的 10**P 和
* 连锁舍入到最近的 10**P 的结果不同。
其中P 是最小的整数,满足10**P ≥ x。
题解:
通过找规律可以发现:
0到100之内有5个数字两种计算方法不一样:45,46,47,48,49
而100到1000范围内不一样的数字为:445到499
1000到10000范围内不一样的数字为:4445到4999
至此可以发现不同范围内计算结果不一样的数字是有规律的,打表即可。
第二题

题目描述:
农夫约翰有一块立方体形状的奶酪块,位于三维坐标平面上,范围是从(0,0,0) 到(N,N,N)(2≤N<1000)。农夫约翰将对这块奶酪进行Q 次(1≤Q≤2*10**5)更新操作。
在每次更新操作中,农夫约翰会从奶酪块中挖去一个1×1×1 的奶酪块,该块的坐标范围是从整数坐标(x,y,z) 到(x+1,y+1,z+1),其中0≤x,y,z
由于农夫约翰在玩一款叫 Moocraft 的游戏,挖去的奶酪块不会受到重力的影响,即使下面的奶酪被挖空,剩余的奶酪块也不会掉落。
在每次更新操作后,输出一种计数:在当前剩余的奶酪块中,农夫约翰可以放置1×1×N 的长砖的不同方式的数量。每种放置方式要求长砖的任意部分都不与剩余的奶酪块重叠,并且长砖的所有顶点必须是整数坐标,且在范围[0,N] 内。农夫约翰可以任意旋转长砖(沿x、y、z 轴放置)。
题目解析:
铜组第二道题目涉及到三维空间的想象,很多学生对于这个三维空间没有概念,自然也就无法理解题目到底想要问什么,怎么样才能达到题目的目标。
这道题目其实是给定一个长度为N的字符串S,最多可以修改其中一个字符,问有多少种形如”ABB”格式的子串,能在S中【不重复】地至少出现F次。
第三题
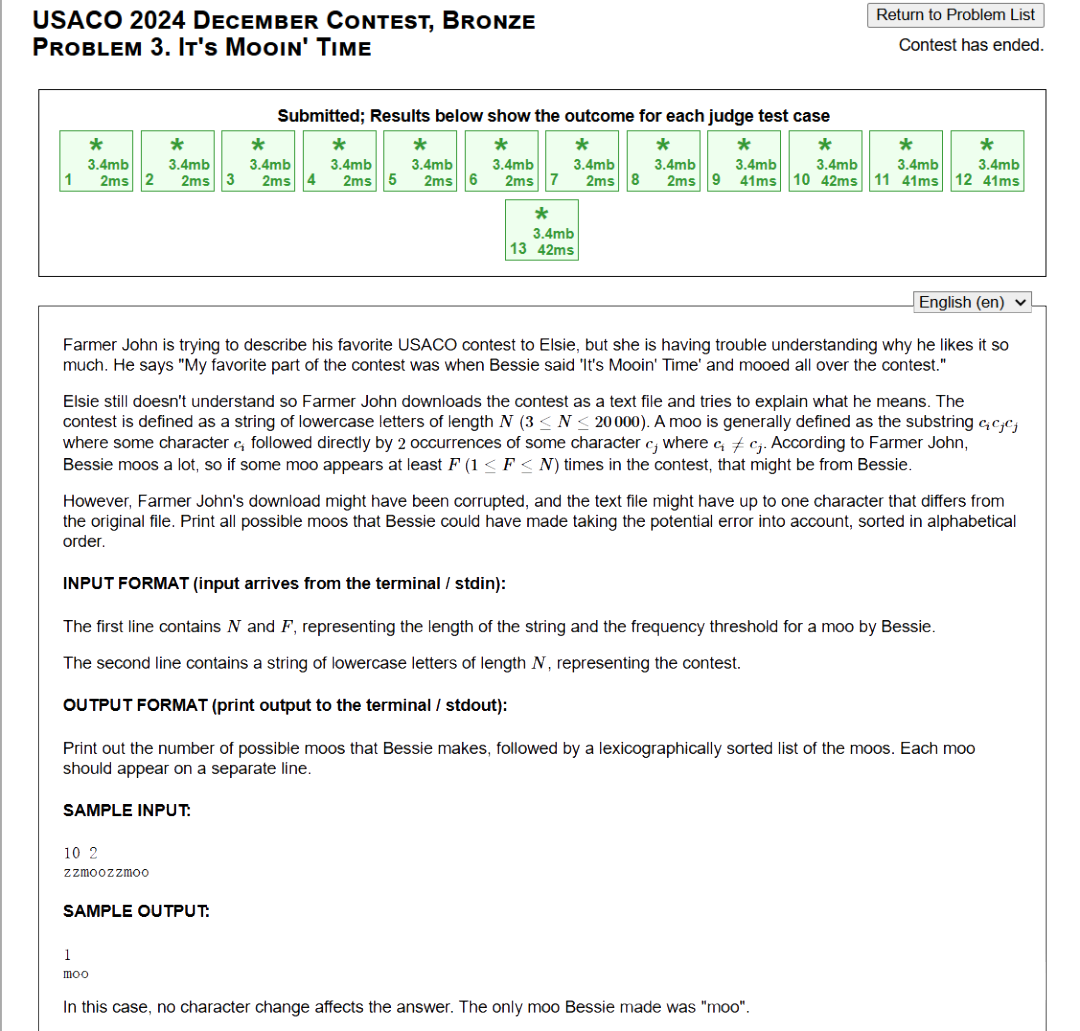
题目描述:
农夫约翰正在向艾尔茜描述他最喜欢的 USACO 比赛,但艾尔茜不明白他为什么这么喜欢。约翰说:“我最喜欢比赛的一部分是,当 Bessie 说‘It's Mooin' Time’并在比赛中‘moo’的时候。”
艾尔茜仍然不理解,于是约翰下载了比赛的文本文件试图解释他的意思。
比赛被定义为一个长度为N(3≤N≤20000)的由小写字母组成的字符串。一个 moo 通常被定义为以下形式的子串:ci cj cj :
* 第一个字符是某个字符 ci ;
* 紧接着是两个相同的字符 cj ,且 ci≠cj
根据约翰的说法,Bessie 经常“moo”,所以如果某个 moo 出现至少F 次(1≤F≤N),那么这个 moo 可能是由 Bessie 发出的。然而,约翰下载的文件可能已经被损坏,文本文件中最多有一个字符可能与原始文件不同。
你需要找出在这种情况下,Bessie 可能发出的所有 moo,并以字典序排序输出。
题目解析:
先枚举所有两个不同字母的组合x和y(ab、ac、ad...、az、bc、bd、be、......、bz、za、zb、zc.....zy),枚举字符串s中所有的连续的三个字母,检查是xyy的话,就在s的复制字符串t中都标记成‘?’。再从剩余的字符串中找到连续的三个字母,如果和xyy这个字符串里面有至少两个相同的,就可以变成xyy,数量就可以+1。如果最终xyy的数量>=f,就统计数量。并最终输出。由于是按照字母从小到大枚举的,不用再额外排序了。
USACO 2024 DECEMBER CONTEST
SILVER(银级)
第一题

题目描述:
Bessie和Elsie发现了N个蛋糕排成一行(2 ≤ N ≤ 5·10^5, N是偶数),每个蛋糕的大小为a[i] (1 ≤ a[i] ≤ 10^9),两头奶牛轮流行动:
- Bessie可以选择相邻的两个蛋糕合并(大小相加)
- Elsie可以选择最左或最右的蛋糕放入自己的储存中
-只剩一个蛋糕时,Bessie吃掉它,Elsie吃掉储存中的所有蛋糕
假设双方都采取最优策略,且Bessie先手,求各自最终能吃到多少蛋糕。
第二题

题目描述:
Farmer John想要扩建他的农场,他选择了Red-Black森林作为地点。这片森林有N棵树分布在数轴上,第i棵树的位置是x[i]。由于环保法律的限制,对于K个区间[l[i], r[i]],必须保证其中至少有t[i]棵树。在满足这些限制的情况下,Farmer John想要砍掉尽可能多的树。
### 输入格式
- 第一行包含测试用例数量T
- 每个测试用例:
* 第一行包含两个整数N和K
* 第二行包含N个整数表示树的位置x[i]
* 接下来K行,每行三个整数l[i], r[i], t[i]表示区间限制
### 输出格式
对每个测试用例输出一行,表示最多可以砍掉的树的数量。
第三题

题目描述:
给定一个 N×N (1 ≤ N ≤ 1000) 的网格,每个格子可以放置四种传送带:
- "L": 向左移动物品
- "R": 向右移动物品
- "U": 向上移动物品
- "D": 向下移动物品
- "?": 未建造传送带
在Q天内(1 ≤ Q ≤ 2×10^5),每天会在一个位置建造一个传送带。需要计算每天结束后,最少可能有多少个"无用"格子(物品放在这些格子上会永远在网格内循环)。
USACO 2024 DECEMBER CONTEST
SILVER(金级)
第一题
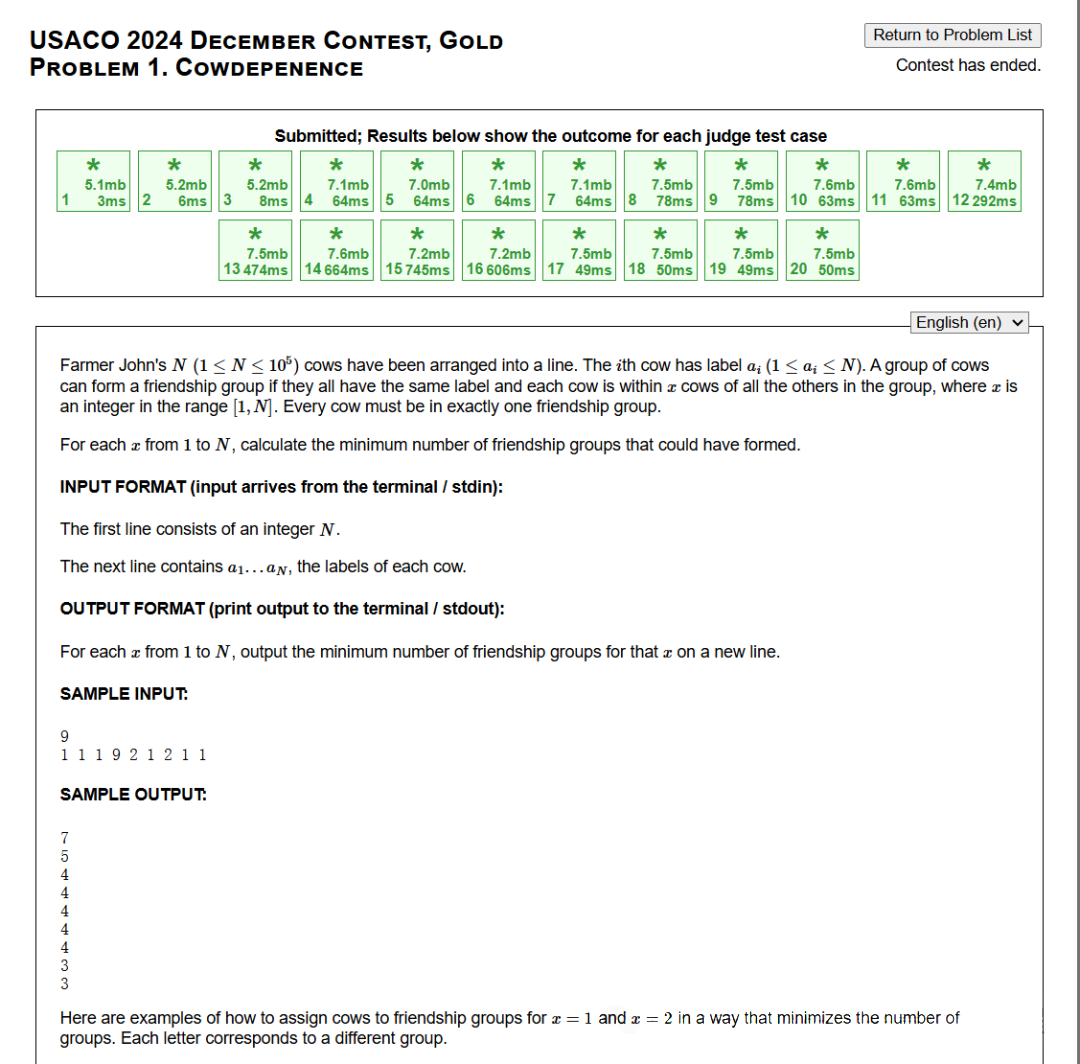
题目描述:
根据题意可知,不同数字之间相互独立,因此可以将每种数字的情况分开处理。 对于每种数字,采用暴力方式处理的时间复杂度为 $O(n)$,因此整体时间复杂度为 $O(n^2)$,这会导致超时。 进一步分析可得,对于某个出现频率为 $k$ 的数字,对应的不同组数的情况很少,且与 $k$ 的数量级相同。 因此,我们可以考虑通过二分查找来优化,当 $x$ 取不同值时,组数发生变化的时刻,时间复杂度为 $O(k log n)$。 综合来看,整体时间复杂度为 $O(nk log n)$。
第二题

题目描述:
考虑定义 `dp[i]` 代表当前考虑了前 `i` 个位置的方案数, $$ dp[i] = sum dp[j] quad (j+1 leq i text,且{ 能够形成一串 R...B...}) $$,在 $O(1)$ Check 合法性的情况下,`dp` 总时间复杂度为:$O(n^2)$,因此需要对 `dp` 进行优化,考虑如何快速计算 `dp[i]`。
我们向前找到第一个 `B` 和第二个 `B`, 就会发现如果这两个 `B` 之间的距离小于第一个 `B` 到 `i` 的距离,那么第一个 `B` 到第二个 `B` 之间是无法形成合法的 `R...B...` 的。
于是我们可以不断向前找,直到找到不满足上述要求的地方,那么对于从那个位置开始往前的一段都是合法的。
对于这一部分我们可以利用前缀和快速转移(寻找上一个 `B` 和 `R` 可以利用 Set 进行查找)。重复执行上述流程,由于每一次长度至少乘 2,总共只会进行 `log` 次,总时间复杂度为:$O(n log^2 n)$ 。
第三题

题目描述:
有n个任务,每个任务有最晚能开始做的时间和完成要需要的时间 ,每个任务开始了就必须做完再做别的。问你从0时刻开始最多能做多少个任务。