美国高中生数学建模竞赛HiMCM!
如此豪横的数学建模竞赛!
美国数学及应用联合会主办
全美一半以上的专业机构资助与认证
数学类含金量最高的国际竞赛之一
世界知名学校的敲门砖……

HiMCM是什么?
No.1、美国初中生数模赛事(简称MidMCM)
美国初中生数模赛事(简称MidMCM),是美国的非营利机构——美国数学及其应用联合会(COMAP)2021年新推出的一项国际性的数学赛事活动,是高中数学建模赛事(HiMCM)的延伸。
MidMCM以团队合作的形式进行,旨在提高14岁以下参赛中学生在团队中的建模能力,解决问题的能力以及锻炼他们的写作技巧。
1、报名人数
赛事由2-4名14岁半或以下在校初中生参加组成,必须来自同一所学校。
2、赛事时间
11月3日—11月16日
3、赛事题目
学生需在一个团队环境中,运用应用数学来解决现实世界中的问题。题目模型在11月3日下午3:00发布,参赛团可选择MidMCM的题目,也可以挑战难度更大的HiMCM题目。
4、奖项设置
特等奖(National Outstanding)
决赛入围奖(Finalist)
一等奖(Meritorious)
二等奖(Honorable Mentioned)
参与奖(Successful Participate)
No.1、美国高中数学建模(简称HiMCM)
美国高中数学建模(HiMCM)是由美国数学及其应用联合会(COMAP)主办的一项国际知名数学赛事。
此外HiMCM不仅需要选手具备编程技巧,更强调数学,逻辑思维和论文写作能力。这项赛事是借鉴了美国大学生数学建模竞赛的模式,结合中学生的特点进行设计的。
1、参赛形式
由最多4名9-12年级在校高中生组成,必须来自同一所学校,配备一位指导老师。
2、赛事时间
11月3日-11月16日
3、赛事奖项
特等奖(National Outstanding):获奖队伍数量不超过队伍总数的1%
决赛入围奖(Finalist):获奖队伍数量不超过队伍总数的7%
一等奖(Meritorious):获奖队伍数量约占队伍总数的12%
二等奖(Honorable Mentioned):获奖队伍数量约占队伍总数的31%
参与奖(Successful Participate):成功完成建模论文的队伍
HiMCM参赛前的注意事项
由于HiMCM赛事是每年的11月开始比赛,次年2月初出成绩,对于申请已经迫在眉睫的12年级同学来说,无论是时间还是精力,都难免有些吃力。
所以大家一定要提前考虑好,HiMCM还是要尽早参加!
要想做出一篇成功的论文,必须要:
掌握数学模型的基本知识,常见的经典模型及算法;
熟悉操作各种计算工具软件和代码,如Matlab,SPSS等;
掌握信息检索、数据查找的技能,会上网找论文;
掌握数学写作软件的编辑和排版,公式编辑器的使用等;
擅长论文写作以及排版。
需要注意的是:
从题目发布到上交最终的论文,只有14天时间。14天光是完成比赛内容就已经非常紧张,完全没有空余再去学习相关的技能。因此必须要在比赛开始前就掌握这些必需的技能!
HiMCM比赛的特(难)点:
●时间说长不长说短不短,最终论文成品看投入多少时间;
●很看队友,单打独斗行不通(基本上都是同校同学的话不会有问题);
●开卷的形式无形中加大了难度;
●如何创新?(O/F奖挑战);
2022年美国数学建模HIMCM比赛时间节点
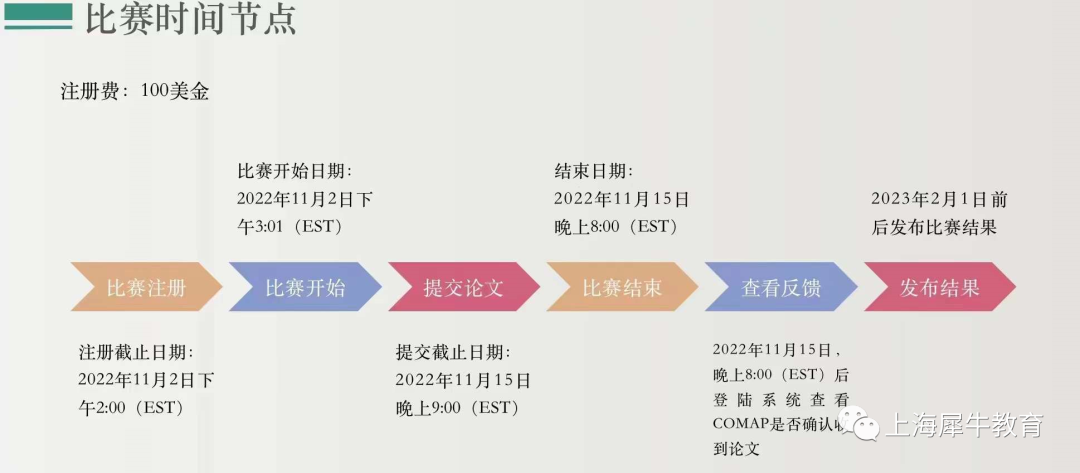
为了能让刚接触HiMCM赛事的同学少走弯路、避免让大家花费了大量时间和经历后空手而归,上海机构老师分享了一些备赛建议:
01、队友很重要!(要仔细核对好信息,确认靠谱【以及档期!愿世界没有撞车惨剧】
ps:经授权,机构可帮忙组队哦~
02、认真上课,精读PastPaper,好好写作业啊朋友们!!
03、10大数学建模常用模型和数学论文排版工具(ex:LaTeX)一定要学的扎实
04、选题非常重要(HiMCM是AB两题,虽然理论上不会出现A非常难但B很简单的情况,但还是有内容和牵扯学科的差距,可能和不同队员的申请方向挂钩)
05、HiMCM的O奖一般只有前1%的队伍才能拿到,难度对于高中生而言是非常大的。无数大佬折戟沉沙,如果没有拿到奖,不要气馁,不要失望,无论结果如何都不会影响你的优秀!
HiMCM课程推荐
1、1V1班适合基础弱,想短期提高分的学生
2、1V3/6小班课基础一般,可以长期学习提分的学生
3、线上学习时间不固定,不适合线下的学生
4、线下基础一般,想要面授教学授课的学生
竞赛课程辅导
适用学员:初高中生
课程目标:完成HiMCM竞赛的知识点的学习。通过系统地梳理,充分的练习熟悉考试的题型和难点重点,冲刺HiMCM竞赛高分
机构竞赛课程大纲
1.综合掌握常见模型的方程求解
2.热传导模型的计算和方法拓展;坐标转换
3.转移状态矩阵,二叉树模型
4.随机微分方程,离散变量的处理
5.普通布朗运动,伊藤过程(Ito Process)
6.可解情况的综合讨论
7.球坐标,广义坐标,简单微分几何
8.弦振动的二阶方程;流体力学问题
9.泊松分布,帕累托分布,其他偏度分布,概率密度函数
10.统计软件的操作,常用回归分析技巧
11.时域有限差分,网格法
12.有限元,大数近似常用办法
13.蒙特卡洛,Bagging,AdaBoost, Bootstrap
14.梯度算法,Logistic Regression,Artificial Neural Network
15.根据学生的具体选题进行针对性指导(生物工程,计量经济,机械,热动力,流体力学等)
16.如何查阅文献,如何引用,如何快速找到自己所属的领域,其他细节
17.数据处理,图表展示的规范和科学性;常用数据处理手段和相关软件的操作指导
18.摘要和总结展望的构思技巧,如何表达研究过程的问题和待完善之处
19.总结