IGCSE数学A、数学B和进阶纯数三门课程的学习内容有什么区别?考试内容的区别是?三者难度有什么不同?分别适合什么样的学生学习?IGCSE数学A、数学B和进阶纯数三门课程的高分率是怎样的?
IGCSE数学
爱德思考试局作为世界公认的三大考试局,其IGCSE数学是一门核心的科目,它开设了数学A、数学B和进阶纯数三门课程。虽然都是数学类科目,但这三门课程有很大的区别,那么,问题来了,IGCSE数学中数学A、数学B和进阶纯数有什么区别?
01、课程内容
IGCSE数学A
IGCSE数学A分为基础(Foundation)课程和进阶(Higher)课程,学生可以根据个人情况进行选择。
基础课程和进阶课程均学习相同的6大模块:
1.数及数系
2. 方程,公式和恒等式
3. 序列,函数和图
4. 几何与三角
5. 向量与变换几何
6. 统计和概率
在具体的分支中,进阶课程会学习一些额外的子主题,例如比例、函数符号、微积分等子主题都是进阶课程会学习,但基础课程不涉及的内容。因此进阶课程的学习内容比基础课程更多,同时难度也更大。
IGCSE数学B
与数学A不同的是,数学B没有基础和进阶课程之分,所有学生将学习相同的课程内容。
数学B课程内容分为10大模块:
1.算术
2.集合
3.代数
4.函数
5.矩阵
6.几何学
7. 求积法
8. 向量与变换几何
9.三角学
10. 统计与概率
IGCSE进阶纯数
进阶纯数课程分为10个模块:
1. 对数函数和指数
2. 二次函数图象
3.恒等式与不等式
4.图表
5.级数
6. 二项式级数
7. 矢量和标量
8. 直角笛卡坐标
9.微积分
10. 三角学
IGCSE进阶纯数的课程内容明显比IGCSE数学A和数学B难度更大,是数学A和数学B的加深和拓展,涵盖了更多的微积分和更高层次的数学理论,适合那些数学基础好,想要挑战自己的学生。
IG进阶纯数与A-level数学在内容上有重叠的部分,如果A-level想继续学习数学或进阶数学,进阶纯数能够为将来的学习奠定更坚实的基础。
02、考试内容
IGCSE数学A
IGCSE数学A考两份试卷,每份试卷各占总成绩的50%,考试时间都是2小时。
基础试卷评分范围为1-5,进阶试卷评分范围为4-9,因此想要拿高分的同学一定要参加进阶考试。
IGCSE数学B
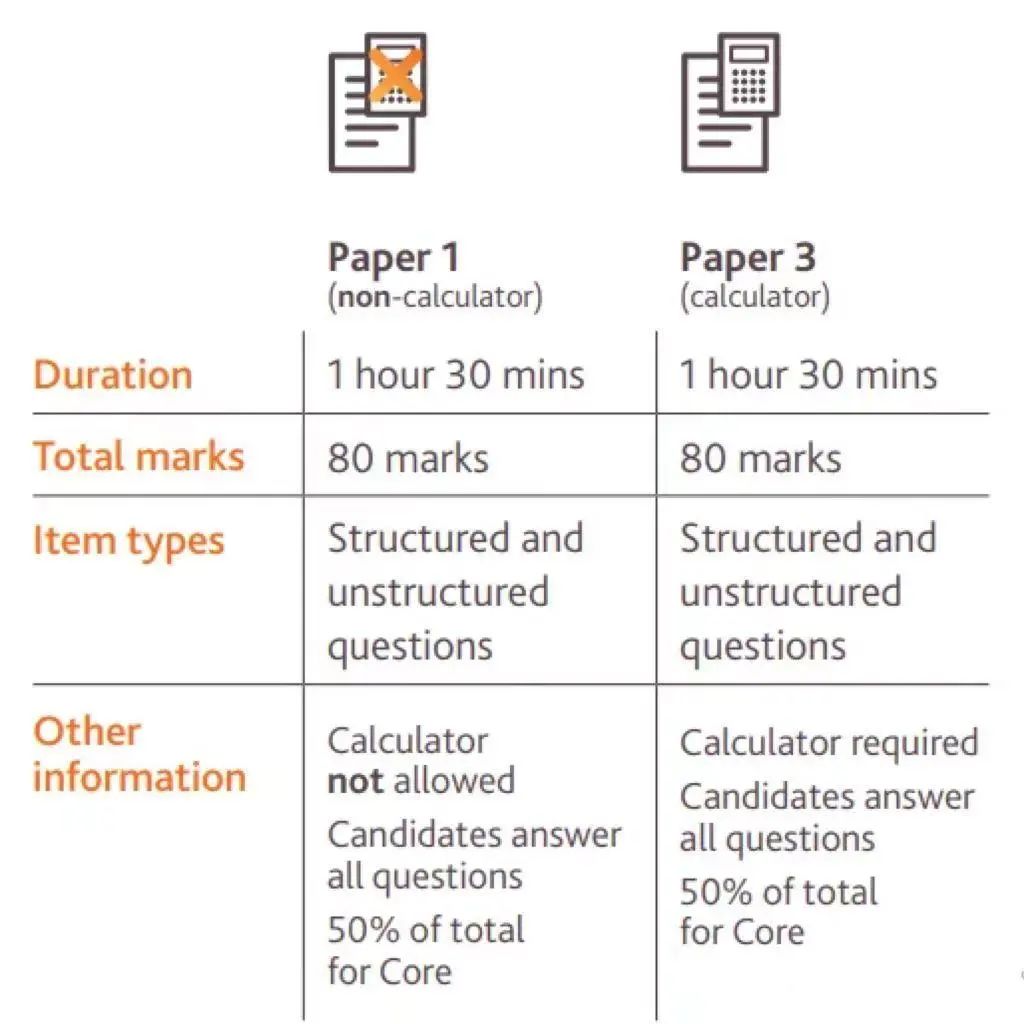
IGCSE数学B考两份试卷,Paper1占总成绩的1/3,考试时间为1小时30分钟。Paper2占总成绩的2/3,考试时间为2小时30分钟。数学B的考试评分范围为9-4(允许3),低于最低成绩标准将得到一个U。
IGCSE进阶纯数
进阶纯数考两份试卷,每份试卷各占总成绩的50%,考试时间都是2小时。
每份试卷包含大约11道题,每道题的分值分配都不同,这将在试卷中进行说明。
进阶纯数的考试评分范围为9-4(允许3),低于最低成绩标准将得到一个U。
03、考试高分率
IGCSE数学A
在2019年夏季考试中,IGCSE数学A有51.4%的考生获得了7/8/9(A-A*)的高分成绩。
IGCSE数学B
2019年夏季IGCSE考试中,数学B获7/8/9(A-A*)成绩的学生比例为53.2%。
IGCSE进阶纯数
2019年夏季的IGCSE进阶纯数考试,有41.2%的考生获得了7/8/9(A-A*)的成绩。
从成绩统计数据来看,最易拿高分的课程是数学B,其次是数学A。相比之下进阶纯数的高分学生比例要更低,不过考虑到进阶纯数的课程难度较大,这也在意料之中。
一般来说,进阶纯数是数学能力较强的学生在数学A/数学B的基础之上额外选修的科目。这门课涉及到很多复杂的公式理论,考试题目也比数学A/数学B要难很多,因此更建议那些具备较强数学能力,或者A-level打算学习进阶数学、数学、物理的学生选修。
数学的重要性再怎么强调也不为过,因为它不仅能为A-level理科科目的学习打好基础,而且是英国大学在录取时十分重视的IGCSE学科,很多顶尖大学的相关专业都要求IGCSE/GCSE数学成绩至少达到C/5,有的大学要求可能会更高。
04知识点部分
一、算术:算术运算的一般过程;质数、因数和倍数;指数、幂和根;根的简单运算;合理化分母;自然数,整数,有理数和无理数;重量、测量和货币;分数、小数、比率、比例和百分数;精确的表示数字;使用上下限来解决问题,这些上下限的值具有一定精确度;标准格式数字
二、集合:集合的概念;集合语言和符号;集合的并集与交集;集合中元素的个数;互补集合;子集合;全集,空集;维恩图及其在简单逻辑问题中的应用;用符号表示集合
三、代数:代数的基本过程;公式的结构、解释、使用及其运算;简单代数表达式的因式分解;因子定理的应用;立方的代数除法;简单代数分数的运算;含一个未知量的一、二、三次方程的解;两未知数线性方程组的解;解有两个未知数的联立方程;线性不等式的解,以及解在数轴和二维空间上的表示;解一个未知数的二次不等式,用数轴表示解集;序列的概念
四、函数:变量函数的概念;函数的作用;使用函数符号;函数的域和范围;复合函数;反函数;变量,直接和间接的比例;矩形笛卡儿坐标;明白y = mx + c的方程是直线图,在点(0,c)处斜率为m,截距为y轴;图形和图形处理方程;绘制图形梯度;x的整数次幂的微分;梯度、变化率、值和最小值、固定点和转折点的确定;应用于线性运动学和其他实际问题
五、矩阵:用矩阵表示数据;矩阵的加法和乘法;矩阵乘以标量;单位矩阵和零矩阵;非奇异2×2矩阵的行列式和逆;平面的变换与2×2矩阵有关;组合的转换
六、几何学:欧几里德空间的几何性质;几何推理;平行线、三角形和多边形(包括正多边形)的角度特性;平行四边形、矩形、正方形、菱形、梯形和风筝的性质;关于点、线或平面的对称性;在二维和三维空间中使用毕达哥拉斯定理;相似图形的面积和体积;证明两个三角形的相似性;相等的形状;理解并使用SSS, SAS, ASA和RHS条件来证明三角形的全等性;圆的弦、角和切的性质;圆内接四边形的性质;二维的轨迹;角平分线和直线垂直平分线的构造
七、求积法:长度、面积和体积;测量二维形状,矩形,平行四边形,梯形,三角形,圆形;三维形状,右圆筒形,右圆锥体和球体,长方体,金字塔,棱镜的测量;弧的长度,圆的扇形的面积
八、向量与变换几何:标量和矢量;向量符号;用有向线段表示向量;平行向量,单位向量和位置向量;两个向量的和与差;向量的模量;向量乘以标量;求两个或两个以上向量的和;将向量方法应用于简单几何;平面变换;组合的转换;向量与矩阵的乘法
九、三角学:使用正弦,余弦和正切的角度达到180°;通过计算和绘图解决二维和三维问题;升降角度;轴承
十、统计与概率:数字数据的图形表示;确定离散数据集的平均值、中值和模式;以分组频率给出的较大数量的平均值的估计值的计算;确定一个模态类和包含分组数据中值的类;了解概率论的语言和基本概念;对两个或多个互斥事件使用加法规则;对两个或多个独立事件使用乘法规则;确定两个或两个以上独立事件的概率;对组合事件使用简单的条件概率;找到简单的条件概率;理解并使用“预期频率”
05对IGCSE数学的学习建议: 在考前,有关的数学学词汇一定熟记于心,在做题的过程中遇到的专业词汇必须用一个专用的本子记下背诵,这原因很简单只有这样我们才能在考试的时候准确的理解题意,更快更精确的解决问题。
误区:一些同学认为IGCSE的数学考试可以在考试过程中查字典,从而为了一时的懒惰而不去掌握词汇,在考试时因心情 紧张且找不到对应的意思忙中出错。
对于考试知识点方面特别强调的几点:
a)矩阵的运算(加、减、乘和逆以及他们可以运算的条件)和简单的变换,虽然这个内容在IGCSE考试中很简单,但从 长远角度来看这部分内容对Further maths中的向量空间内容的理解很有帮助。
b)概率问题是我们很容易混乱的问题,但只要同学彻底的弄懂对立事件、互斥时间、相互独立事件以及他们的运算法则 就可以了。不会做就画树状图
c)累计频数图一定要搞定,这个部分是难点,几个基本的概念一定要清楚,比如:upper guartile and low quartile inter-quartile range,mean等,会看图并且根据图来判断数据。
d)直方图是必考内容,会读图。
e)圆的内容大家比较熟悉,但是因为平时用的很少搞得大家很陌生,要求大家多作复习。 f)体积和比例问题要细心,比如各种体积公式的理解和应用、相似比的平方等于面积比、立方等于体积比等不多说。
g)尺规作图问题要清楚了解,角平分线和中垂线的做法要熟练。
h)三角函数中的正弦定理和余弦定理不容忽视。
i)向量是我们第一个接触的由大小和方向两个元素决定的量,很容易出错。
i)其他内容就很简单基本上不粗心就可以做的很好。