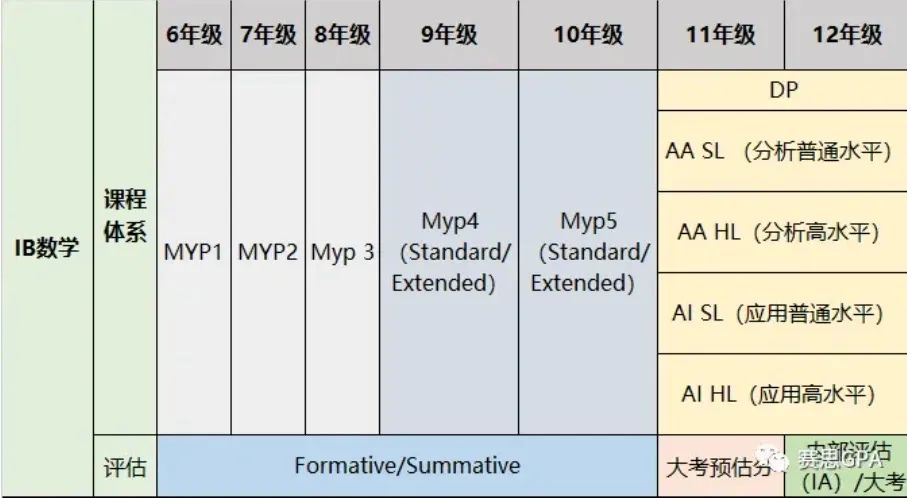
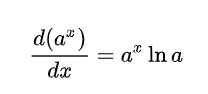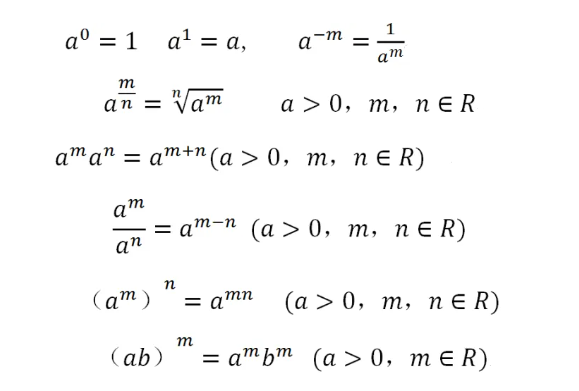提到MYP数学,很多人都觉得苦不堪言。因为学校往往没有明确的教材或题集,也没有正式的考试来做课程评估,所以很难get到自己的掌握程度。
这其实是很危险的一件事!很多同学和家长在10年级即将选课的时候都表示:压根不知道自己的数学水平是什么样,到底选AA数学还是AI数学呢?多选理科类还是人文社科类的课程呢?选HL还是SL呢?
要知道,等到了11-12年级,IB数学的难度直接拔高了一个档次,排名和口碑靠前的大学更是只看数学HL的成绩,仅两年的时间里还要兼顾科学和人文社科课程,其实是没有足够的时间让大家慢慢适应新的学习强度的!
也就是说,学生在MYP阶段,就需要培养思维的灵活性和多变性,多用一题多解、一题多变的形式,对同样的问题进行发散性思考,想出多种解决问题的方法。
这一阶段打好基础,不仅可以作用于高年级数学、物理、经济、心理等众多学科,还能够长远地帮助同学们培养未来工作和学习必备的数学技能和思维方式,作用于论文撰写和学术研究。
既然说到“基础”,那肯定绕不开函数。此前老师给大家总结过MYP数学最难的三角函数和圆定理的知识点,今天想和大家分享指数函数的相关内容。
因为三角函数和指数函数是数学中两个重要的函数概念,它们之间存在着一定的联系和关系,可以相互转化,除了会在微积分部分有所涉猎,指数函数更是被广泛应用在经济商管中,是IBers绕不开的重要难点!
那么下面就开始今天的学习吧~
指数函数学习要点
MYP数学的难度呈螺旋式上升,但内容基本上是统一的,数字(number)、代数(algebra)、几何与三角函数(geometry and trigonometry),统计与概率(statistics and probability)这四大领域是每年、每学期都要接触的。
那么我们需要做的就是学习新知识的同时,不断将前后的知识结合起来思考,消除不同年级、不同学段之间的知识断档,建立条理清晰的知识框架,学会在各种实际问题中挖掘本质,寻求数学的方式进行解决。
MYP数学 • 指数函数
*图片来自网络
1、基本概念
指数函数(Exponential function)属于数学中的基本初等函数之一。
一般地,y=a^x (a为常数且a>0,a≠1)叫做指数函数,函数的定义域是R。其中,a是底数(或称基数,base),x是指数(index / exponent)。
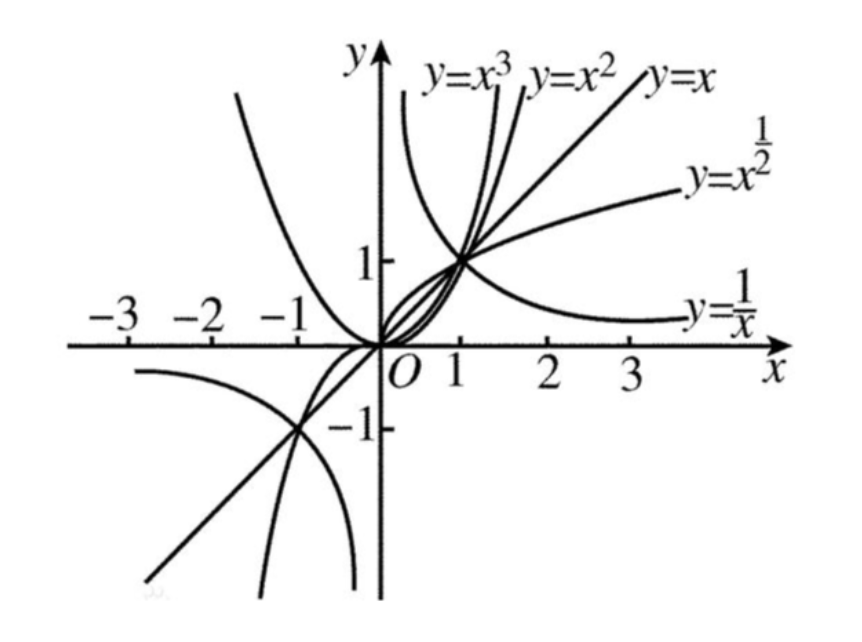
当a>1时,指数函数对于x的负数值非常平坦,对于x的正数值迅速攀升,当x=0时,y=1;
当0<a<1时,指数函数对于x的负数值迅速攀升,对x的正数值非常平坦,当x=0时,y=1;
在x处的切线斜率=此处的y*lna,即:
*图片来自网络
2、指数的基本性质
•指数函数的定义域为R,并且以“a为常数且a>0,a≠1”为前提;
•指数函数的值域为(0, +∞),因为底数是>0且≠1的常数,所以无论x取何值,都意味着有x个a相乘,所以结果肯定是大于0的;
•函数图形的单调性:a>1时,函数是单调递增的,在第一象限,底数越大,增长速度越快;0<a<1<时,函数是单调递减的,底数越小,递减速度越快。
• 指数函数为非周期性、非对称性的凹函数;
• 指数函数是非奇非偶函数;
• 指数函数有反函数(对数函数)。
3、幂的比较
一般来说,最常用的方法就是以下四种:
• 通过指数函数图像的单调性来判断;
•做差法:m-n>0,即m>n | m-n=0,即m=n | m-n<0,即m<n,注意变形和定号;
• 做商法:m/n>0,即m>n | m/n=0,即m=n | m/n<0,即m<n,注意m和n的值要大于0;
•中间值法:要比较m与n的大小,先找一个中间值q,再比较m与q、n与q的大小,由不等式的传递性得到m与n之间的大小关系。
另外还需注意:
•对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;
•对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图像的变化规律来判断。
4、指数的基本运算法则
指数函数的基本运算法则需要多加练习🤓🤓
*图片来自网络
【乘法法则】
• 同底数幂相乘,底数不变,指数相加。
•幂的乘方,底数不变,指数相乘。
•积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
•分式乘方,分子分母各自乘方。
【除法法则】
•同底数幂相除,底数不变,指数相减。
•任何不等于零的数的零次幂都等于1;任何不等于零的数的-m(m是正整数)次幂,等于这个数的p次幂的倒数。
5、专项训练提升
指数函数的相关内容对于MYP 8-10年级的学生来说,还是很有挑战性的。
因为指数函数的内容不会单独出几道题考察,而是会融合在各项大题的几个小问当中,融合其他知识点一起考察,跨度很大。
另外,指数函数与三角函数的内容相结合,将会直接决定大家DP阶段的微积分部分能不能学透彻,而且与数学分析、物理学、工程学等方面都有很大的作用!
MYP数学 • 高分思路
◀统筹规划▶
如果将MYP数学的内容按照年级来细化和拆解,可以发现各年级的学习重心是不同的。
【6年级】
上学期围绕数字的具体概念去展开,运用加、减、乘、除以及分数和小数这些基本运算,下学期推进到代数和概率单元。
【7年级】
7年级拓展负数和有理数下的四大基本运算,比率和比例、单步和多步代数、二维和三维物体、面积、表面积和体积等知识点都要掌握。
【8年级】
8年级开始以主题为学习单元,集中在代数和几何上,重点培养分析思维和推理逻辑,为高年级DP的数学学习打下基础。
【9年级】
9年级的各个主题和8年级是紧密相连的,主要涵盖了数值、代数和几何主题。
【10年级】
10年级依旧是围绕几何、三角函数、概率、向量、二次函数和统计这几大主题,但难度上升,要做好衔接准备。
◀找准重点▶
MYP数学,重难点有很多,但是占大头的还得是圆定理和三角函数,尤其是三角函数部分,与DP和大学数学必修的微积分息息相关,甚至有学生说“数学微积分的尽头即为三角函数”。
所以,MYP阶段分专项的训练尤为重要!