2022AP 物理C电磁学北美卷FRQ真题解析及难度分析

2022年5月10日进行的AP物理C电磁学考试已经结束，本场考试为线下纸笔考试，CB官网已更新了2022AP物理C电磁学北美FRQ真题。

2022年的AP物理C电磁考试已经结束，今天官方放出了两个Set的FRQ，我们赶紧一起来看看都考了哪些内容吧！

试卷整体难度和知识点

两个Set的相同题号考的知识点相近，第1题都是在考高斯定理和电场电势的微积分关系，只不过Set 1是球对称模型，Set 2是柱对称模型；

第2题都是在考RC电路的实验，都涉及了微分方程，且都是先充再放，只不过Set 1根据对数电压-时间图像求电容，Set 2是根据时间常数-电阻图像求非理想电容的内阻，但也都考了实验误差分析和图像斜率变化；

第3题都是在考电流产生的磁场和电磁感应，主要涉及磁场、磁通量计算、法拉第定律和楞次定律，只不过Set 1是长直导线周围的不均磁场需要用积分计算磁通量，Set 2是螺线管里的匀强磁场，但都考了条件改变时感应电流的变化分析。

整体难度中等，有的题非常简单并且和往年题目极为相似，有个别问题较为新颖或有小坑。

与往年题目对比的点评

电场的题目应该算简单，2018年第1题也是绝缘球外面套一个导体球壳，用高斯定理算电场并画图，而柱对称模型2013年也出过。

RC电路的先充后放问题去年刚刚考过，只不过去年更侧重多个电阻电容串并联的分析，而今年都是一个电阻一个电容，但在实验设计和数据分析上做文章。

磁场的题也非常常规，Set 1非均匀磁场的磁通量去年MCQ考过，国际卷2017模拟题FRQ第3题也有，而Set 2螺线管电流变化在线圈中产生感应在2019年Set 1的第3题也有考到，只不过2019年是线圈套在螺线管外，今年是线圈塞在螺线管里。这样看来，如果同学们在考前刷过2018、2019、2021三年北美FRQ真题，对今年的考点应该都有所应对。

逐题点评

因为两套题相同题号的考点类似，所以逐题点评按大题号顺序进行，每个序号内分别讲解Set 1和Set 2的两版题目。

FRQ 1

Set 1: 一个均匀带负电的绝缘球外面套了一个同心带正电的导体球壳。

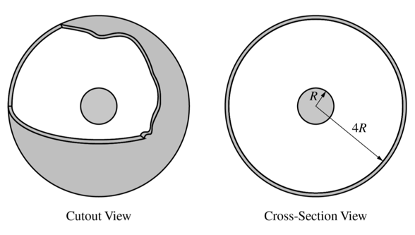
(a) 求导体球外表面的电荷。

考点：导体静电平衡，高斯定理，电荷守恒。

思路：根据静电平衡的性质，导体内部没有电场，根据高斯定理，球壳内表面电荷与绝缘球加起来为0。再根据电荷守恒得到外表面电荷。

(b) 推导绝缘球内部的电场表达式。

考点：高斯定理，电荷体积密度。

思路：在球内做同心球型高斯面应用高斯定理。电场在高斯面上处处相等且与面垂直，电通量为电场乘以球面积；内部包围的电荷量等于电荷体积密度乘以包围的小球体积，其中体积密度可以用总电荷除以总体积得到。

(c) 已知绝缘球表面电场，求绝缘球和导体球壳中间某处的电场。

考点：高斯定理，平方反比规律。

思路：在绝缘球和导体球壳中间做高斯面应用高斯定理可得电场遵循平方反比规律，距离变成两倍则电场变成1/4。

(d) 求绝缘球表面和导体球壳内表面的电势差绝对值。

考点：电场电势关系。

思路：对电场积分即得电势差。

(e) 分别画出电场和电势与到球心距离的函数关系图像。

考点：高斯定理，电场电势关系。

思路：根据高斯定理可以先求得电场的变化规律（前几问已求出一部分），再根据电场等于电势的负导数，可以从电场确定电势图像的斜率如何变化，从而画出电势的变化趋势。例如电场如果为负（指向球心）且线性增大，那电势的斜率为正且增大，为上凹曲线。

Set 2: 一个无限长均匀带正电的绝缘圆柱外面套了一个同轴带正电的导体圆柱壳。

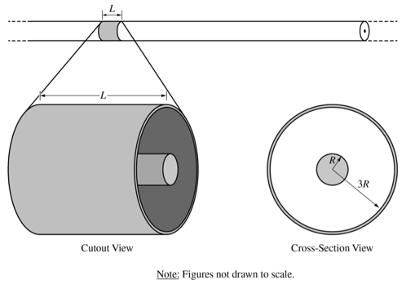
(a) 求一段导体圆柱壳外表面的电荷。

考点：导体静电平衡，高斯定理，电荷守恒。

思路：根据静电平衡，导体内部没有电场。根据高斯定理，圆柱壳内表面电荷与绝缘圆柱加起来为0。再根据电荷守恒，得到外表面电荷。

(b) 推导绝缘圆柱内部的电场表达式。

考点：高斯定理，电荷体积密度。

思路：在圆柱内做圆柱形高斯面应用高斯定理，电场在侧表面上处处相等且垂直于侧表面，电通量为电场乘以圆柱的侧面积；内部包围的电荷量为电荷体积密度乘以包围的小圆柱体积，其中体积密度可以用总电荷除以总体积得到。

(c) 已知绝缘圆柱表面电场，求绝缘圆柱和导体圆柱壳中间某处的电场。

考点：高斯定理，反比规律。

思路：在绝缘圆柱和导体球圆柱壳中间做高斯面应用高斯定理可得电场与到轴线距离成一次反比规律，距离变成两倍则电场变成1/2。

(d) 求绝缘圆柱和导体圆柱壳内表面的电势差绝对值。

考点：电场电势关系。

思路：对电场积分即得电势差。

(e) 分别画出电场和电势与到轴线距离的函数关系图像。

考点：高斯定理，电场电势关系。

思路：根据高斯定理可以先求得电场的变化规律（前几问已求出一部分），再根据电场等于电势的负导数，可以从电场确定电势图像的斜率如何变化，从而画出电势的变化趋势。例如电场如果为正（沿半径向外）且线性增大，那电势的斜率为负、电势减小，且绝对值增大，为上凸曲线。

FRQ 2

Set 1:用一个可变电容研究放电时的电压变化。给了一个理想电池，一个电压表，一个电阻，第一个可变电容，和若干开关。

(a) 画一个电路图，既可以用来给电容充电，还可以用来研究放电电压。

考点：RC充放电电路。

思路：电路中应该至少包含两个回路，一个包含电源用于充电，一个不含电源用于放电，两者共用一个电阻-电容支路。需要至少两个开关，一个控制充电，一个控制放电。另外电压表应该并联接在电容器两端。

(b) 证明放电时电容器电压随时间变化的函数表达式。

考点：基尔霍夫定律，RC电路的微分方程。

思路：对RC放电回路列基尔霍夫定律，把电流i写成dq/dt得到微分方程，求解出q(t)进而得到V(t)。需要注意两点：

(1)电流正方向规定为流向正极板才有i=dq/dt，实际放电电流为负；如果规定放电电流方向为正，则i=-dq/dt。

(2)电容器放电的初始电压等于充满电的稳态电压，亦等于电源电压。

(c) 根据实验数据画出了散点图，纵轴为电容电压与初始电压之比的自然对数ln(V/V0)，横轴是时间，让我们画出最佳拟合线，并用其求电容。

考点：指数函数线性化，最佳拟合线斜率的利用。

思路：将上一小问的表达式变形后可以得到直线的斜率所代表的物理量是-1/RC，画出拟合线后，在线上取两点求斜率，C=-1/(R*slope)。

(d) 调节可变电容器的平行板面积，重复实验，问直线的斜率会更陡峭、更平缓、还是不变，并解释原因。

考点：电容的决定式，改变条件下的斜率分析。

思路：根据电容决定式，面积增大，电容增大；再根据斜率=-1/RC，C增大斜率绝对值减小，所以是less steep。

(e) 将理想电池换成一个有内阻的电池，问斜率和截距是否变化，并解释原因。

考点：非理想电源的内阻，RC放电。

思路：电源的内阻不会改变充电时的稳态电压，也不改变放电电路的时间常数，所以图像的斜率和截距都不变。

Set 2: 做实验确定一个非理想（含内阻）电容器的内阻。给了一个理想电池，一个电流表，一个可变电阻，第一个电容，和若干开关。

(a) 画一个电路图，既可以用来给电容充电，还可以用来研究放电电流。

考点：RC充放电电路。

思路：电路中应该至少包含两个回路，一个包含电源用于充电，一个不含电源用于放电，两者共用一个电阻-电容支路。需要至少两个开关，一个控制充电，一个控制放电。另外电流表应该与电容器直接串联。

(b) 证明放电时通过电容器的电流随时间变化的函数表达式。

考点：基尔霍夫定律，RC电路的微分方程。

思路：对RC放电回路列基尔霍夫定律，把电流i写成dq/dt得到微分方程，求解出q(t)进而得到i(t)。需要注意两点：

(1)电流正方向规定为流向正极板才有i=dq/dt，实际放电电流为负；如果规定放电电流方向为正，则i=-dq/dt。

(2)电容器放电的初始电压等于充满电的稳态电压，亦等于电源电压。

(c) 根据实验数据画出了散点图，纵轴为时间常数τ，横轴为可变电阻的阻值R，让我们画出最佳拟合线，并用其求电容。

考点：时间常数，最佳拟合线斜率和截距的利用。

思路：在上一小问的表达式中可以看出时间常数τ=(R+r)C，变形后可以得到直线的斜率所代表的物理量是C、纵截距所代表的物理量是r*C，画出拟合线后，在线上取两点求斜率得到C，找纵轴交点求截距，则电容内阻r=intercept/C。也可以反向延长找到直线与横轴负半轴的交点直接得到内阻，但因为给定的坐标格不包含负半轴所以一般不这么做。

(d) 如果电流表也有内阻，试分析电容器的真实内阻与实验值的差异。

考点：电流表内阻，误差分析。

思路：如果电流表有内阻，实验值应为电流表内阻和电容器内阻之和，大于电容器内阻。

(e) 改变可变电阻器的电阻范围，问斜率如何变化。

考点：改变条件下的误差分析。

思路：改变横坐标的取值范围，斜率不变，仍是C。

FRQ 3

Set 1: 一个连有灯泡的矩形线框放在通电长直导线附近，导线中的电流先减小再反向增大。

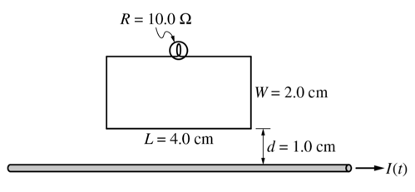
(a) 问直导线电流反向时矩形线框中感应电流的方向。

考点：电流产生的磁场，楞次定律。

思路：根据右手定则，直导线在上方线框中产生的磁场是先向外减小、再向里增大的。根据楞次定律，感应磁场应该一直向外，不要被“反向”这个瞬间迷惑。再根据右手定则判断感应电流方向为逆时针。

(b) 计算某时刻线框中的磁通量。

考点：不均匀磁场中磁通量的计算。

思路：直导线周围的磁场和距离成反比，需要用微元法，将线框分成无数个细横条，计算每个面积微元上的磁通量，再积分。

(c) 计算某时刻通过灯泡电流。

考点：法拉第定律。

思路：利用上一问的方法得到磁通量随时间变化的关系，根据法拉第定律计算感应电动势，除以电阻即得到电流。

(d) 测量发现实际电流比上一问的计算值大，选择一个可能的原因。

考点：法拉第定律。

思路：直导线中电流变化得比预期快会导致线框中磁通量变化率偏大，从而感应电流偏大。

(e) 将矩形线框旋转90度使短边平行于长直导线，比较同一时刻的感应电流和c问中的大小。

考点：电流产生的磁场，磁通量，法拉第定律。

思路：距离到导线越远磁场越小，旋转后更多面积微元远离导线，总磁通量和电流的比例系数变小，感应电动势和感应电流也相应变小。

Set 2: 一个单匝线圈放在螺线管中，螺线管的电流在线性增大。

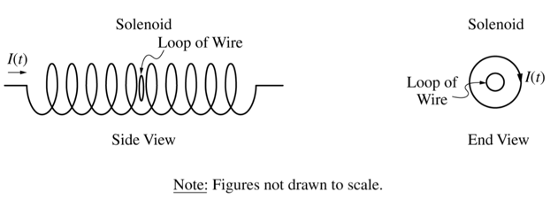
(a) 问线圈中感应电流的方向。

考点：电流产生的磁场，楞次定律。

思路：根据右手定则，在侧视图中螺线管在线圈中产生的磁场是向里增大的。根据楞次定律，感应磁场应该与之相反向外。再根据右手定则判断感应电流方向逆时针。

(b) 计算某时刻线圈中的感应电流。

考点：磁通量计算，法拉第定律。

思路：根据螺线管磁场公式计算线圈中磁通量，再根据法拉第定律计算感应电动势，再用欧姆定律得到电流。

(c) 计算一段时间线圈消耗的能量。

考点：能量和功率。

思路：利用感应电动势或感应电流得到功率，乘以时间得到消耗的能量。

(d) 测量发现实际电流比b问的计算值小，选择一个可能的原因。

考点：法拉第定律。

思路：线圈平面与螺线管轴线不垂直会导致磁通量变化率偏小进而感应电流偏小。

(e) 将线圈半径变成两倍，问感应电流和b中的比值。

考点：磁通量，法拉第定律，电阻的决定式

思路：线圈半径变两倍，面积变4倍，感应电动势变4倍。但是题目暗示了我们线圈周长变成了2倍，电阻也变成了2倍，所以感应电流应该只变成2倍。

写在最后

以上就是北美考情的分析了，对于备考明年考试的同学来说，应当注意对基础公式和模型的掌握，AP的出题风格并不会有太激进或太灵活的变化，和课内的呼应比较好。不过需要基本功扎实，尤其是公式推导和微积分的计算要足够熟练。