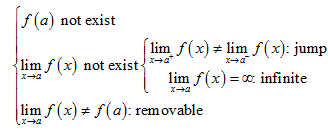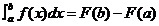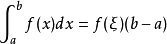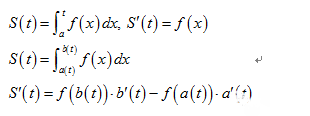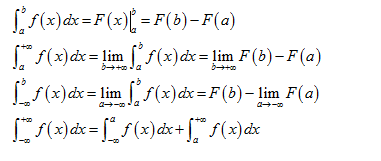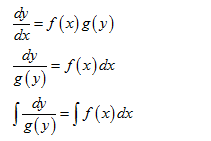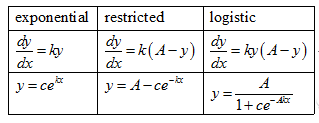AP微积分,是一门美国大学预修课程,其成绩不仅可以抵扣成功申请美国大学的同学们入学后相应课程的学分,还被作为美国各大学录取学生的重要依据,所以考到一个好的分数,成为了很多同学的愿景。好消息是AP微积分的难度整体不大,好好备考,拿到5分的可能性还是很大的~
备考重点
基础不牢,地动山摇
虽然在平时我们鼓励大家适当拓展一些有用的技巧和知识点,但是大考当前还是基础最为重要。AP面向的是全球的美高体系学生,虽然中国学生卷到不行,但是也不会针对此而猛提难度,不过近几年也略有提高的趋势,所以大家还是不要掉以轻心。基础知识掌握到位,理解通透,才能灵活应对考题,毕竟所有的题目归根到底都是万变不离其宗的。
真题不看,等于白干
任何的考试真题要是被辜负了,出题老师都会很伤心的OK?(开个玩笑) 考试真题是非常珍贵的备考资料,因为它充分体现了命题组对于大纲的把握和对于课程目标的理解,做真题能帮助你理解命题组出题的角度和考察的内容,因此大家一定要认真对待真题,将错题整理好,学会举一反三,有空多回顾一下。
计算不好,高分不保
AP微积分考试分为四个部分,其中非计算器部分的分值占比远高于计算器部分,足以见得计算的重要性,若你在平时写题或者上课的习惯就是只看不写,那么你真的需要改正。只有动笔计算了,你才能发现原本以为没问题,实际上根本不会写的地方,才能暴露出你的知识漏洞。切记,考前发现问题不是一件坏事,相反正因为意识到了,你才有机会改正,才有机会更上一层楼,避免来年二战。
知识点梳理
1、极限部分
考点:(1)判断极限存在与否,存在时如何求出该极限
(2)渐近线(asymptote)与连续性(continuous)的考察。
1.1 极限存在的判定标准
左极限与右极限均存在且相等
note:极限不存在的可能情况——左右极限不相等、无穷大、震荡
1.2 求极限的方法
1.2.1 分母因式分解
1.2.2 洛必达法则(0/0及∞/∞时)
1.2.3 等价无穷小的替换
常见等价无穷小有:x ~sinx ~tanx ~arcsinx ~arctanx ~ln(1+x) ~e^x -1
(1+x)^a -1 ~ x^2/2
1.2.4 灵活运用幂指函数
1.2.5 0*有界函数可视为0(无加减时)
1.3 极限的应用
1.3.1 连续性:若函数在某一点的极限值等于该点函数值,则称函数在该点连续,即左极限=函数值=右极限
1.3.2 间断点类型:
1.3.3 连续性三定理:
1.3.4 渐近线
水平渐近线:x趋于无穷时(正无穷或负无穷),函数极限为常数值
垂直渐近线:x趋于a时(左极限或右极限),函数趋于无穷
2、导数与微分
核心考点:如何求导及导数的应用
2.1 导数与微分的定义
简单来说,导数是切线的斜率(slope),微分是切线的改变量。
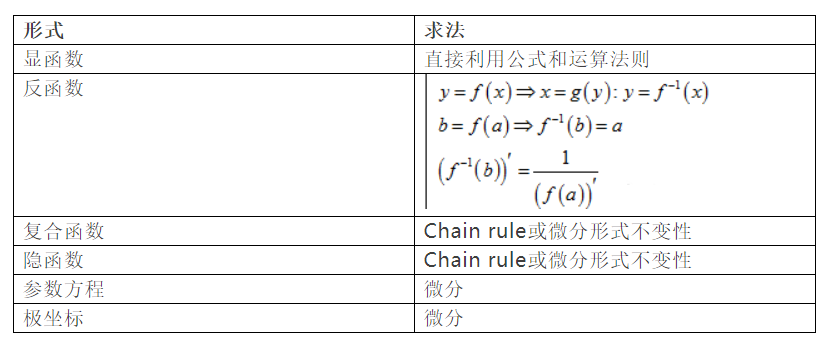
2.2 求函数不同表示形式的导数
2.3 高阶导数
先求低阶导,再对其求导
2.4 可导与连续
可导必连续,但连续未必可导(e.g.y=|x|在x=0处连续但不可导)
2.5中值定理
从几何图形上来看,当函数在闭区间上连续、开区间内可导时,必然存在一点c使得过c点切线的斜率等于端点连线的斜率。
3、导数与微分的应用
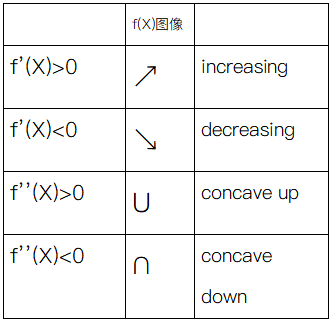
3.1 函数图像与导数的关系
3.2 极值与最值
极值(local/relative maximum and minimum):领域内最大或最小
求极值步骤:求出一阶导数等于0和不存在的点→利用一阶导数是否改变符号和二阶导数的正负来判定。
最值(global/absolute maximum and minimum):整个区间内最大或最小
求最值步骤:求出一阶导数等于0和不存在的点→求出所有的函数值和端点值,最大的即为global max,最小的即为global min。
4、不定积分和定积分
考点:(1)如何求不定积分 (2)如何求定积分
4.1 不定积分
4.1.1 换元法(substitution):将被积函数的某一部分用另外的变量代替,从而将被积函数化简,使用积分基本公式得出结果。
4.1.2 分部积分法(integral by parts):适用于求两类不同函数乘积的积分,核心是通过交换来改变被积函数,从而将难求的变成容易求的。
4.1.3 有理函数积分:对于分母是1次和2次的形式有固定的套路,掌握即可。
4.2 定积分
4.2.1 定积分思想--黎曼和(Riemann sum)
使用近似逼近的方式来求面积,常用的是左端点、右端点、中点、梯形来做估计,步骤如下
(1)将区间等分成n份(也可不等分)
(2)按照预先设定的规则求出每一部分的面积
(3)加总
4.2.2 牛顿-莱布尼茨公式
notes:配合使用换元法时,变量取值范围应随之变化;灵活使用奇函数与偶函数的性质。
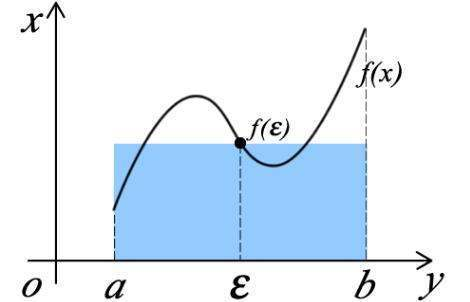
4.2.3 积分中值定理
如果函数 f(x) 在积分区间[a, b]上连续,则在 [a, b]上至少存在一个点 ξ,使下式成立:
其中(a≤ξ≤b)
4.2.4 变限积分
4.2.5 反常积分(improper integral)
当积分区间不是有限区间(即包含无穷大)或积分区间会使被积函数为无界的时候,求积分需要用到极限,如果极限存在,则称积分收敛(converge),不存在则称为发散(diverge)。
5、定积分的应用
5.1 求面积
求平面曲线围成的平面图形的面积,一般来说是给定一条或若干条曲线,求它与x轴、y轴或其他直线或曲线围成图形的面积。
对于直角坐标系,使用定积分的几何意义来求,但需要注意的是面积永远是正数,而积分值有正有负,因此当函数大小关系或区间的边界发生变化时,要注意区别对待。
5.2 求体积
求平行截面面积已知的立体图形的体积和旋转体体积,第一种图形对截面面积求积分可得体积,第二种图形有两种求法,第一种也是对截面面积求积分,不过要注意旋转截面是实心圆还是圆环,第二种是利用shell来求,掌握好展开后的圆柱壳的长宽高即可。
5.3 求弧长
弧长公式用四种,一般来说在考试中如果是不允许使用计算器的部分,只会要求考生列出计算公式,不要求算出数值,而允许使用计算器的部分则可利用计算器来计算弧长的数值
6、微分方程
6.1 求解微分方程
对于可分离变量的微分方程,通常将x与y分离后对等式两边同时求积分
6.2 slope field
根据微分方程原函数每一点切线斜率计算出来,而后将与该点切线斜率相同的线段画在坐标系中,由此所形成的图形即为slope field。斜率场所描绘出的图形即为微分方程的解。
6.3 增长模型
指数型增长(exponentialgrowth)
有限制的增长(restrictedgrowth)
逻辑斯蒂增长(logisticgrowth)
6.4 欧拉估值(Euler's method)
多次使用中值定理进行估值,此时c不再任取,而是固定取每一步的起始值
7、级数
7.1 无穷级数
分为正项级数(positive)、交错级数(alternating)。
这部分的核心是如何判断一个级数是收敛(converge)还是发散(diverge)。
7.1.1正项级数(positive)
判别法有三类五种,分别是积分(integral)、比值与根值(ratio and root)、比较及极限(comparison and limit comparison)。
7.1.2 交错级数(alternating)
莱布尼茨准则(Leibniz)
收敛(converge)分为绝对收敛(absolute converge)和条件收敛(conditional converge)。
7.1.3 判定顺序
(1)将级数加绝对值取正
(2)对通项求极限,若极限不等于0,则可判定为发散,若等于0,则(2.1)利用积分(integral)、比值与根值(ratio and root)、比较及极限(comparison and limit comparison)判定,若收敛,则原级数绝对收敛,若发散,则(2.1.1)若原级数为交错级数,利用莱布尼茨准则判断,若收敛,则为条件收敛,否则为发散。
7.2 幂级数
利用比值法求出收敛半径(radius of convergence)和收敛区间(收敛域)(interval of convergence)。
幂级数的性质:
幂级数在收敛区间内(1)连续(2)可微(3)可积。
7.3 泰勒级数
(1)将函数展开为泰勒级数
(2)求泰勒级数的和函数