AP微积分FRQ题目分析及知识点盘点

提到AP微积分，可以说是最受中国考生欢迎的科目了，也是AP理科中的5分率王者之一。很多学微积分的同学一开始就是冲着5分去的，然而，考试本身还是有一定难度的，为了确保自己能稳稳拿下5分、不在考试的时候因为各种因素丢分，咱们在备考的时候一定不能掉以轻心，毕竟一年只有这么一次考试机会！

今年的微积分考试时间在5月9日 8 a.m.，没错，只剩最后两周的备考时间了！??时间紧迫，大家要抓紧身边所有可用资源充分备考！

说到AP考试，MCQ和FRQ里肯定是FRQ最让大家头疼——题干又臭又长、要求又多又繁琐，考试范围灵活，难题、怪题、偏题层出不穷。而且，这么难的FRQ，在考试中的分值比重还很高！

可以称得上是5分路上的绊脚石了。

不过大家不要被困难绊倒，这里给大家准备了两道微积分FQR题，快来检测一下你对FRQ题型的熟悉程度以及对知识点的掌握度～

做完后再根据解析分析一下FRQ题目的侧重点，查看自己是否有遗漏的知识点~

第 一 题

解析

我们先来看题目给的条件:

• 1) 0至4的闭区间f有定义

• 2) f的一次导

(a)问的是在哪个区间f是增长的，我们知道[f increasing→f'>0][f decreasing→f'<0]。

所以现在用图形计算器画出f'的图像，大概找出在0至4的闭区间的范围内，f'=0和f'>0的分界点。

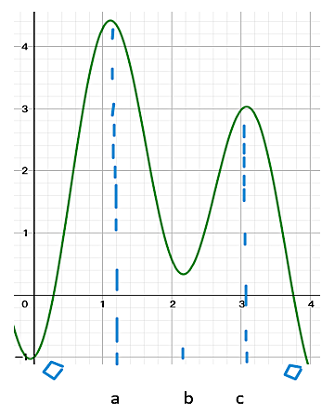
通过画图（如上图）我们得出，在大概0.282和3.758的区域内，f'>0。用到图形计算器的求解功能，我们可以较准确地算出前面的区间在保留三位小数后是(0.283，3.760)。答案就是：On the open interval between 0.283 and 3.760, f is increasing.

(b)问x是什么值时，f有局部极大值。

注意与globalmaximum 区分：一个函数可有多个local max/min，但是只可有一个global max/min。

看回刚刚用图形计算器画的图，我们知道，在(0,0.283)区间，f值减小；在(0.283，3.760)区间，f值增大；在(3.760,4)区间，f值减小。看着f'图在三个区间所包围的面积来看，在(0.283，3.760)区间包围的正面积最大，所以在当x=3.760时，f有最大值。答案就是：f has a local maxima when x=3.760

(c)问的是，在图上有几个拐点。

Inflection point就是函数改变concavity的时候：例如从concave up(f''>0)变成concave down(f''<0)。这道题只问了数量，并没有问确切的位置，所以步骤相对简便。

可以看出，在f'的x=a,x=b, 和x=c前后的地方，f''发生了变化。0到a这一段f''>0；a到b这一段f''<0；b到c这一段f''>0；c到4这一段f''<0.因为f''发生了三次变化，所以一共有三个inflection point。答案就是：f has 3 inflection points.

（误区：不小心把f'的图当成了f的图像，直接找concave up/down的图形）

第 二 题

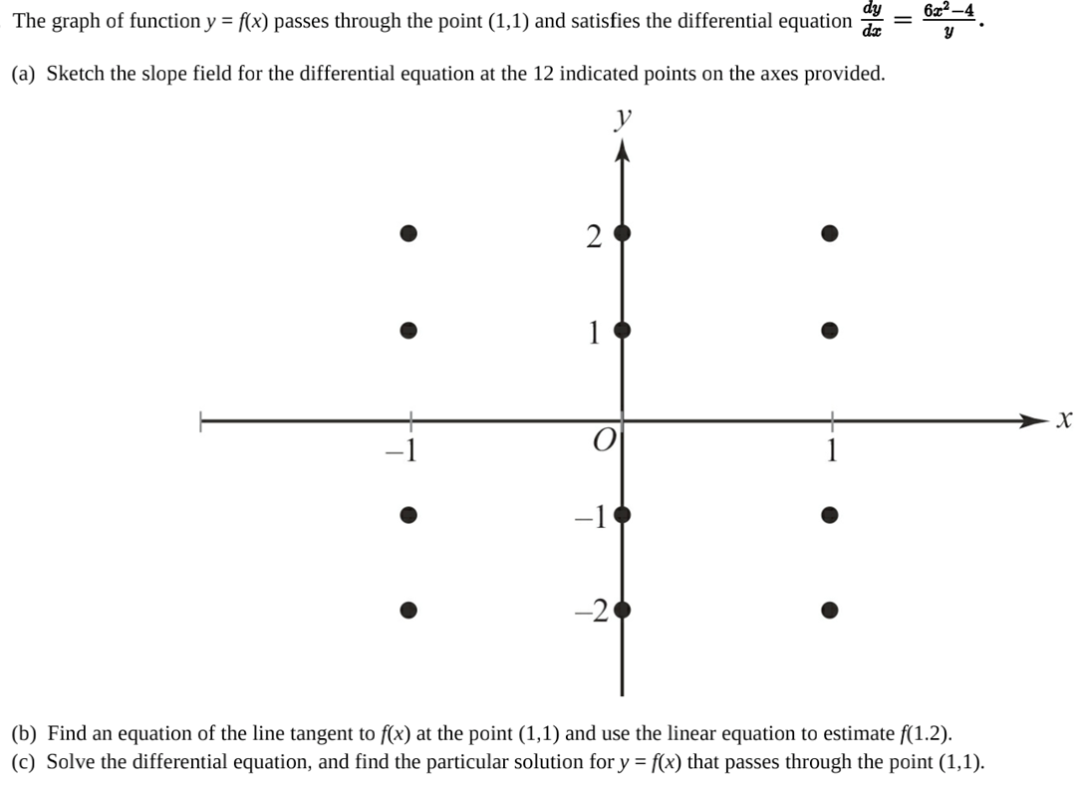
解析

本题中的(a)问要求我们在图内画上斜率场。

我们只需要把点对应的坐标带进微分方程里根据数值画出每个点对应的斜率就好了（如上图）。不需要非常准确，但是对于不同的斜率要肉眼可辨别出来。

(b)问要求用我们通过(1,1)的数据写出equation来估算f(1.2)。

已知在(1,1)时，dy/dx=2。切线的方程列出来是y-1=2(x-1)→y=2(x-1)+1.[通式是y-y1=(dy/dx)(x-x1)--(x1,y1)为用来估算值的点]现在我们只需要把x=1.2代入，就能得出f(1.2)≈2(1.2-1)+1=1.4 答案是：f(1.2)is approximately 1.4.

(c)问要求我们找出particular solution。

Differential equation 里有两种solution：general solution和particular solution。General solution就是把微分方程进行积分直接得到的式子（有+C），而particular solution 是在此之后将某点代入式子得出来的。步骤如下：

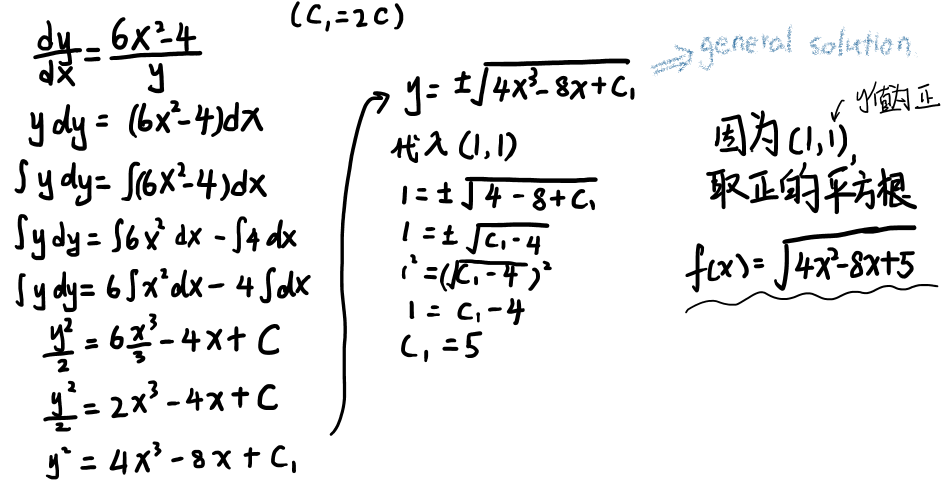
希望通过以上的两道练习，大家能对微积分FRQ的题目设置和易错点有了更清晰的认识。