AP统计5分冲刺攻略：估计estimation知识点分析

在上一期的推送中，我们一起了解了假设检验(hypothesis testing) —— 一种基于收集到的样本数据推测总体参数的方法——我们还使用这种方法尝试验证了各种各样的假设。

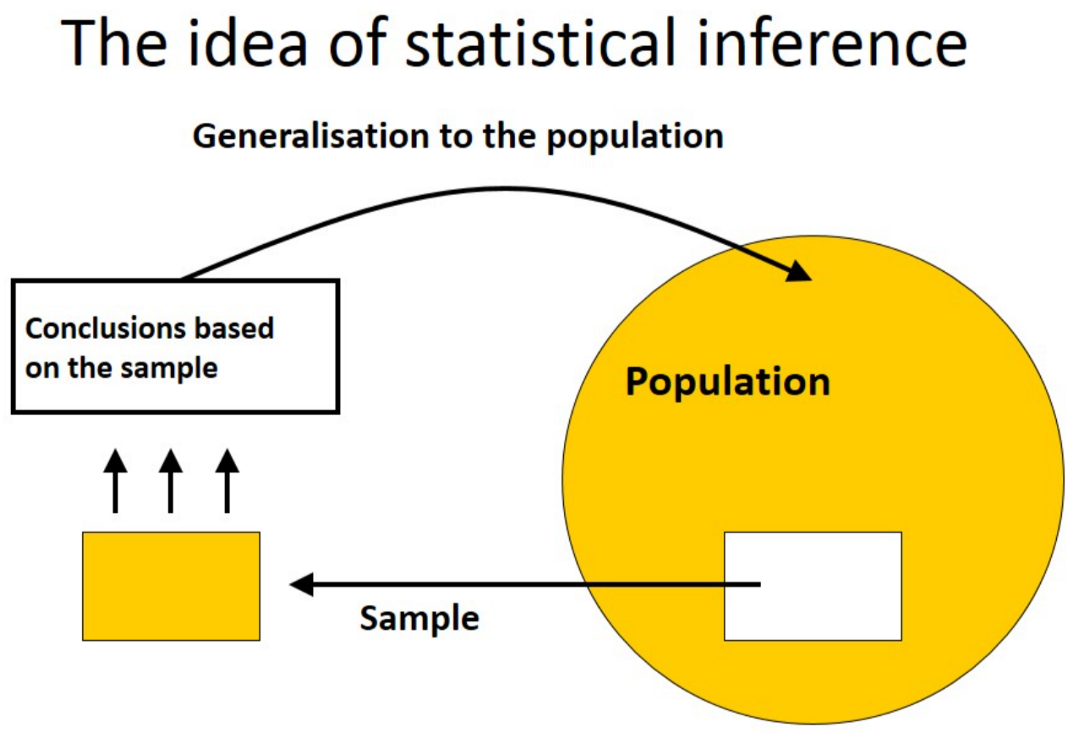
但是呢，假设检验其实只是其中一种进行统计推断(statistical inference)的方式。今天，我们将要在我们的统计推断工具箱里加入另一种有用的工具——估计(estimation)。

本 文 目 录

1.Estimation

• Point Estimator

• Interval Estimator

2.Confidence Level& Confidence Interval (CI)

• Introduction

• Construction of CI

A. CI for proportion

B. CI for mean(σ known)

C. CI for mean(σ unknown)

3. Choosing Sample Size

Estimation

由于因为收集总体数据是一件非常费时费力的事情，所以我们常常会通过收集样本的方式去推测关于总体的情况。我们进行估计(estimation)的目的，其实就是想要通过样本数据(sample statistic)确定总体参数(population parameter)的粗略值。

有两种不同类型的估计量(estimator)可以供我们使用：点估计量(point estimator) 和区间估计量(interval estimator)。让我们一起来康康它们的区别吧！

1、Point Estimator

假如在我生日那天，我收到了一盒超级大盒的巧克力，我想知道在这盒巧克力里，我最爱的抹茶味巧克力大概占多少比例，我应该怎么做呢？把一块块巧克力都拿出来实在是太麻烦了，所以我打算先吃个10块巧克力，然后数一下这10块巧克力里有几块是抹茶味的。

吃完后我发现这10块巧克力里有一半都是抹茶巧克力，根据这个样本，我推测抹茶巧克力占这整盒巧克力的50%。

在这个例子中，我通过样本数据（10块巧克力里，50%是抹茶巧克力）所推测出的总体参数（抹茶巧克力在整盒巧克力里的占比）“50%” 就是一个点估计量，因为它是一个精确的数字，而不是某个含糊的范围。

图1

【重点概念】

Point Estimator(点估计量):a single number based on sample data that is used to estimate a population characteristic（见图1）. 概念理解就好，不需要记忆，能与interval estimator (区间估计量)区分即可！

不过呢，你可能会想到，虽然我刚才吃的10块巧克力里有50%的抹茶巧克力，但如果我再吃10块巧克力，或许只能吃到1块抹茶巧克力，那么我得到的点估计量就变成10%了。确实，我们在不同的样本中可能会得到不同的数据，从而得到不同的点估计量。

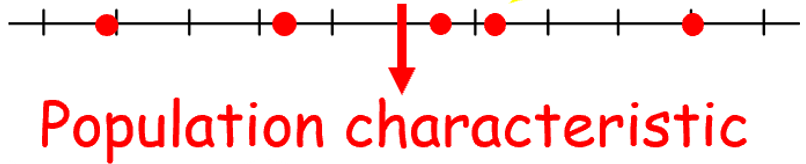
图2

在图2中，我们可以观察到，有些点估计量与总体参数相差无几，但有些点估计量却差了十万八千里，这就与我们所选择的样本的质量有关系。

那么什么样的样本能够给我们更准确、更接近总体真实情况的估计呢？

一个好的样本至少要满足两个条件：

1）它是无偏的(unbiased)；

2）它的变异性(variability)较小。

如果一个样本的抽样分布(sampling distribution)平均值等于总体参数分布的平均值，我们就可以说这个样本是无偏的(unbiased)。

在图3中，蓝色的曲线代表总体参数的分布情况，绿色和红色的曲线分别代表两个不同的样本抽样分布。相比红色的样本，绿色的样本是一个更好的样本，因为它的抽样分布平均值正好与总体分布的平均值相等，是无偏的。

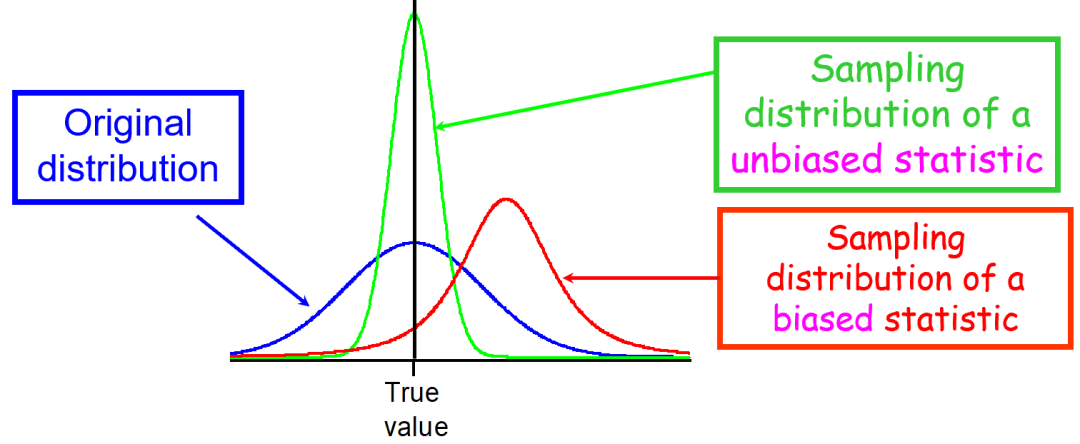
图3

但是，如果我们有几个无偏的样本可以选择，这时候选择哪一个样本更好呢？

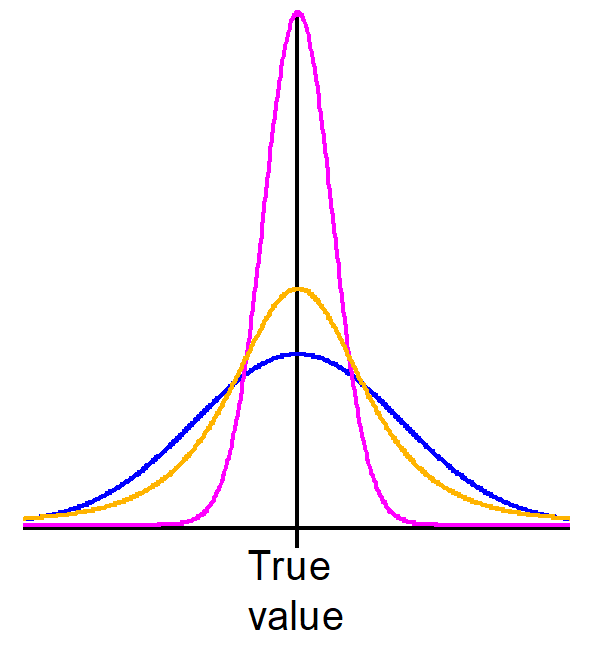
图4

在这种情况下，我们要选择变异性(variability)最小的样本，也就是数据标准差(standard deviation)最小的样本。

在图4中，蓝色的曲线依然代表总体参数的分布情况，粉色和橙色的曲线分别代表两个不同的样本抽样分布。因为这两个样本都是无偏的，所以我们要通过观察它们的标准差进行判断。对一个抽样分布而言，它的形状越高越瘦，标准差越小；越矮越胖，标准差越大。因此，我们应该选择分布形状最高最瘦的粉色样本。

2、Interval Estimator

再让我们回到抹茶巧克力的例子。当我得到点估计量（估计抹茶巧克力在整盒巧克力里的占比）50%时，我有多大的把握呢？

其实我是没有太大把握的，毕竟一下就能找到总体参数的确切值是很难的。但是，如果我推测抹茶巧克力在整盒巧克力里的占比大概是在40%-60%之间，我对自己的预测是否会更有信心呢？

答案是肯定的。因为让我们预测的某个区间包含总体真实参数，一定比直接找到那一个具体的总体真实参数要更容易一些。这里的40%-60%就是一个区间估计量(interval estimator)：一个关于区间的预测，见图5。

图5

Confidence Level & Confidence Interval (CI)

1、Introduction

区间估计量有一个特殊的名字，叫置信区间(confidence interval)。一个总体参数的置信区间，指的是一个包含了所有对这个总体参数的估计值的区间，换句话说，就是我们预测总体参数会落在我们所构造的置信区间上。

【重点概念】

Confidence Interval(CI): a confidence interval for a population characteristic is an interval of plausible values for the characteristic.

尽管相比点估计量，我们对自己所估计的置信区间会更有信心，但别忘了，我们始终是在做一种预测和估计，很难100%确定我们所做的估计一定能够反应总体的真实情况。对于不同的区间大小，我们会拥有不同的信心程度。

想想看，如果现在请你盲猜我的身高，比较140-180cm,150-170cm, 160-165cm,163-164cm这几个你有可能会给出的置信区间，你对哪个区间最有信心呢？或者说，你认为哪个区间最有可能包含我的真实身高呢？

我们会发现，相比其他三个区间，我们应该对140-180cm最有信心。也就是说，置信区间越大，我们的信心程度应该会更高，因为越大的置信区间可以包含越多的可能性，也越有可能将真实值包含在里面。

现在我们将要介绍一个与置信区间相关联的概念：置信水平(confidence level)。

和我们对某个区间的信心程度不同，置信水平反映的是我们对构造置信区间所用的方法的信心程度，或这个方法的成功率，它的数值等于：在构造总体参数的多个样本区间中，包含总体参数的区间占总数之比。

是不是有点抽象？让我们来试着通过分析一个具体的置信水平来理解它的含义。

一个85%的置信水平代表着什么呢？下面这幅图（图6）展示了基于20个随机样本所构建的20个置信区间，总体参数值(true proportion) 表示为图中绿色的横线。有一些区间包含了总体参数值(successfully capture)，有一些却没有(miss)。如果我们认真数一数，就会发现：20个区间中，有17个置信区间成功地包含了总体参数值，占总区间的85%。

这意味着，我们用同样的方法随机抽取20个样本，构造了20个置信区间，其中有85%的区间成功包含了总体参数值，成功预测了总体参数值所在的范围。这就是confidence level = 85%所表示的含义。

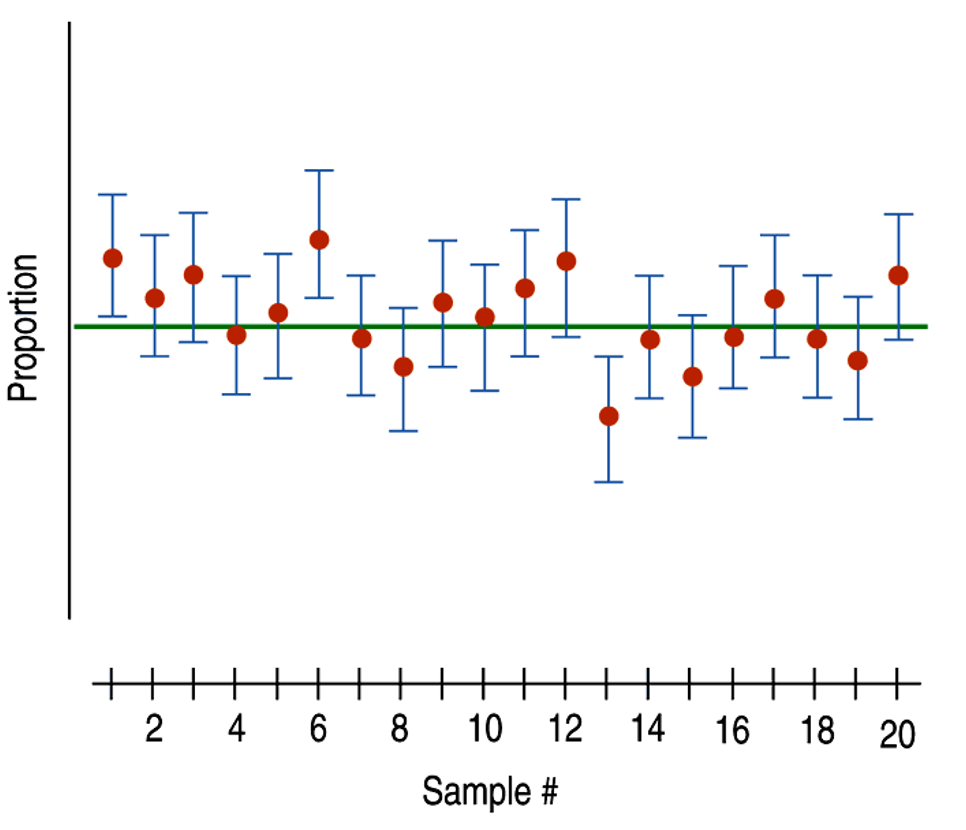
图6

【Tips提示】

在我们构造置信区间的过程中，所使用的常见的置信水平包括：90%,95%, 99%。

【重点概念】

Confidence Level:The confidence level associated with a confidence interval estimate is the success rate of the method used to construct the interval.

概念不要求记忆，但要理解！注意置信水平指的是我们对构建某个置信区间所用的方法的信心程度，也指用这个方法所构造的置信区间包含总体参数的成功率。

【考点提示】

FRQ和选择题都有可能考察我们是否能够解释特定confidence level 的含义。如果FRQ让我们“explain the meaning of n% confidence level in the question”，大家可以使用这个模板：

• ?If many,many samples are selected and many,many confidence intervals are calculateds,about n% of them will capture the true (题目想要推测的 population parameter) .

1、Construction of CI

接下来，我们将学习如何构建一个置信区间。置信区间的大小总是和某个置信水平相关联，我们设置的置信水平越高，在这一水平下构建的置信区间就会越宽，因为一个比较大的区间包含总体参数值的可能性越高。

让我们以95%的置信水平为例，来构造它所对应的置信区间吧！

首先，我们要利用正态分布表查找，当中间的面积占整个正态分布曲线的95%时，中间面积的两个边界所对应的z-score。因为正态分布曲线以下的面积合为1，当中间面积占0.95，两边两个相等的面积就应该各占0.025，然后查表可以得到两个边界的z-score为-1.96和1.96，见图7。

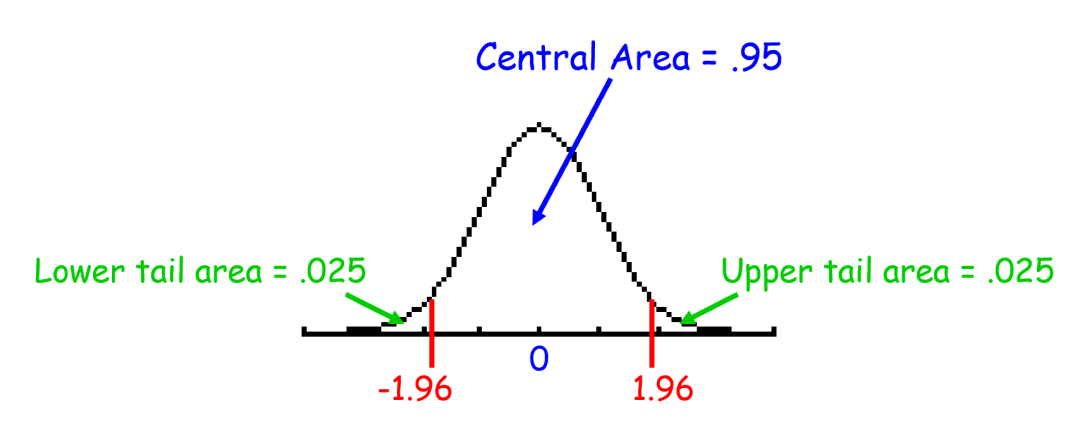
图7

当样本数量n足够大或总体分布呈正态分布时，我们就可以说这些样本所构成的抽样分布(sampling distribution)近似呈正态分布，如果我们对所有样本数据进行标准化(standardize，计算出这些数据的z-score)，这个抽样分布就可以用图7表示。

一个数据的z-score= n的意思是：这个数据离平均值的距离等于n个标准差。

所以我们在上文计算出的两个临界值z-score就代表着：如果样本所组成的抽样分布成正态分布，95%的样本数据会落在“这个分布的平均值±1.96个标准差”这一区间内。这就是置信水平95%所对应的置信区间。

在上文我们提到过，置信水平描述的是我们对自己所使用的构造置信区间的方法所拥有的信心大小，也就是说，假设我们抽取很多个样本，我们可以利用这些样本构造无数个同样大小的置信区间，而我们相信95%的这些区间可以成功包含总体参数。

为什么当我们在抽样分布上计算出一个区间，使得95%的样本数据落在这个区间上，我们就可以说这就是置信区间，代表在无数个样本区间中，其中95%可以包含总体参数呢？

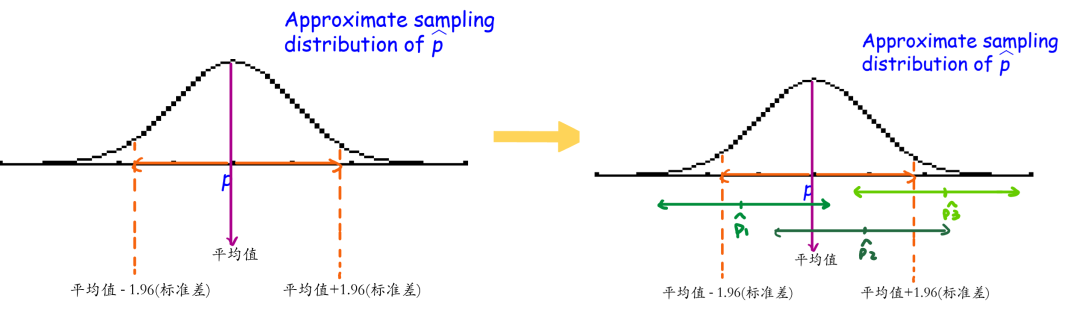
图8

【考点提示】

有时候FRQ也会让我们解释某个特定置信区间(CI)的含义。

我们的解释一定要包含两个关键点：

1）这个置信区间所对应的置信水平(CL)；

2）区间本身。

这边给大家提供一个好用的句式：

• ? I am n%(CL) confident that the true proportion/mean(二选一，取决于数据类型)value of (题目想要推测的population parameter) is contained within the interval (__ , __)(CI).

了解了构造置信区间的原理后，推测它的计算公式就变得非常容易啦！针对不同的数据类型，计算公式会稍有差异，让我们来逐一看看吧~

• A. CI forproportion

如果我们想要预测的总体参数是离散型数值变量(discrete numerical variable)，那么这个参数和收集到的样本数据应该由proportion（比例）表示。

在抽样分布(sampling distribution)一章中，我们知道关于proportion的抽样分布有三个特点：

在我们探索构建置信水平为95%的置信区间时，我们得到了这样一个区间：平均值±(1.96)标准差，我们其实可以把它推广到构建其他置信水平的区间上。那么，我们就可以得到置信区间的计算公式：平均值±(critical value)(标准差)。

当我们要构建proportion的置信区间时，我们可以把一个样本的平均值和标准差带入，得到：

【Tips提示⚠️】常见的置信水平所对应的zcritical value是：90%--- 1.645，95%--- 1.96，99%--- 2.58，记下来可以节省计算时间！

• B. CI for mean (σknown)

如果我们想要预测的总体参数是连续性数值变量(continuous numerical variable)，那么这个参数和收集到的样本数据应该由mean（平均值）表示。

关于mean的抽样分布有三个特点：

同构建proportion的置信区间非常相似，mean的置信区间应该是：

• C. CI for mean (σunknown)

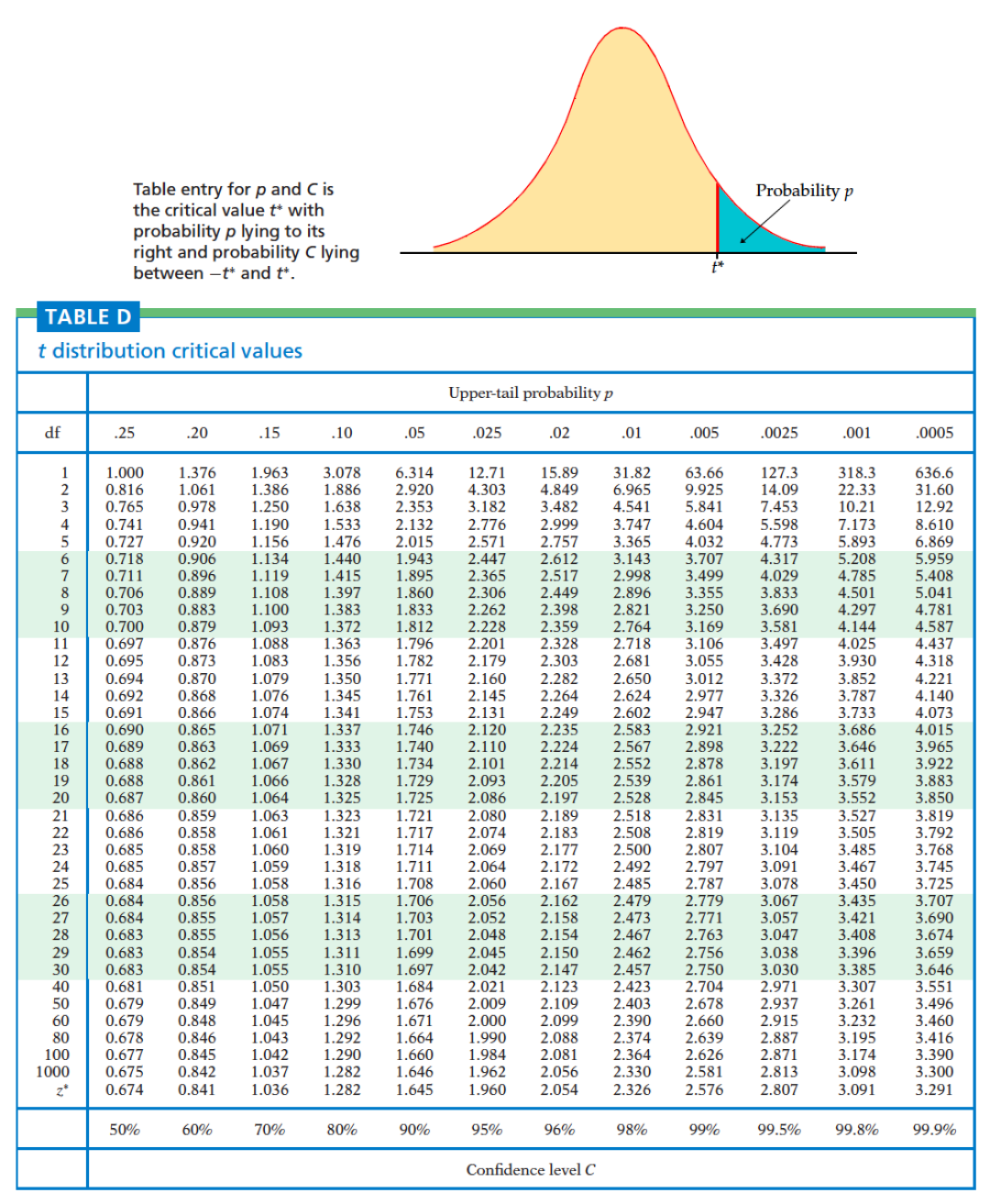
图9

【重点概念】

不需要记忆，只是为了辅助大家理解！

• t-distribution: the probability distribution that estimates the population parameters when the sample size is small and the population standard deviation is unknown.

• degree of freedom (df): the maximum number of logically independent values, which are values that have the freedom to vary, in the data sample.

解析

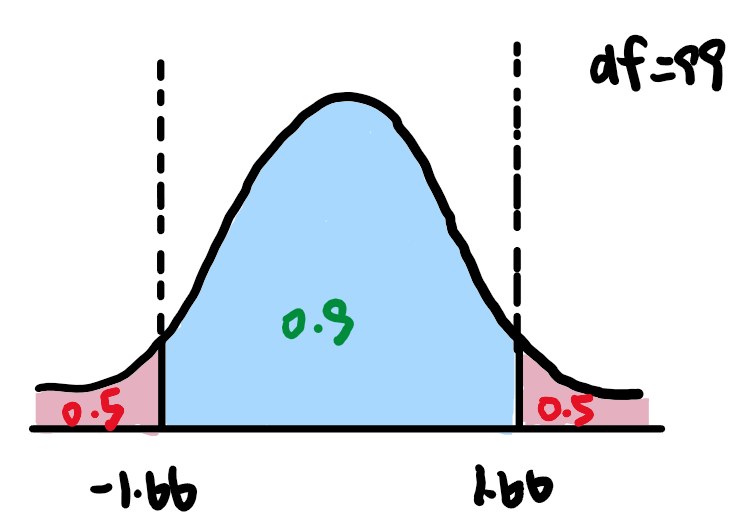
图10

Choosing Sample Size

在开始收集样本之前，我们要先确定，为了在我们所选择的置信水平上对总体参数进行预测，我们至少要收集多少样本量(sample size)，毕竟收集样本是一件费时费力有时还费钱的事情，但样本量过小又会影响我们预测的准确度。

我们可以用“平均值±(critical value)(标准差)”来构造置信区间，其中“(criticalvalue)(标准差)”叫做边际误差(margin of error,ME)，因为这个值代表着对平均值的偏离大小。当我们选定了自己可以容忍的误差范围，也就是确定了ME的大小后，就可以计算最小样本量(minimum sample size)了：

这时候你可能会问了：我怎么知道p和ó的值是多少呢？不就是因为对总体一无所知，我们才会去收集样本进行推测的吗？

确实，但我们也只是在对可能需要的样本量做粗略的估计。虽然我们不知道p和ó的准确值，但我们可以估计，比如先进行一个小范围的预研究(preliminary study)或者基于过去的经验和研究数据。如果我们真的没有任何相关经验，我们可以对p进行一个最保守的估计，假定p=（1-p）=0.5，因为这时p和1-p的乘积是最大的（见图11），可以保证相对大的样本量，使我们得到较为准确的结果和预测。

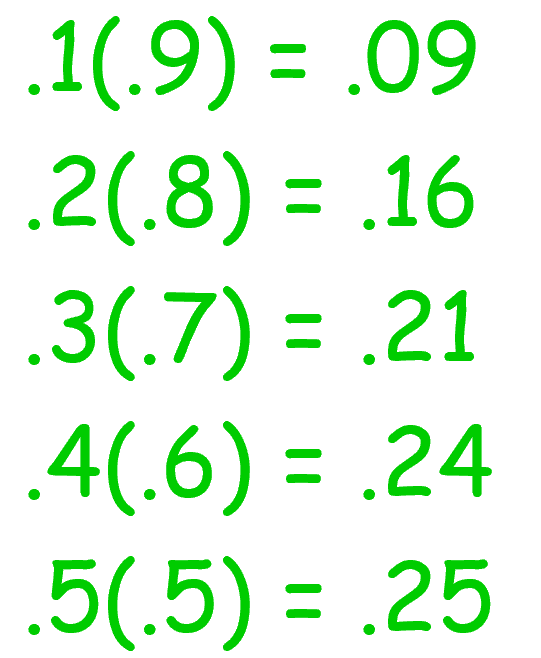
图11

对于ó来说，公式ó≈range/4可以近似估计它的值。（至于为什么，感兴趣的同学可以前往https://www.thoughtco.com/range-rule-for-standard-deviation-3126231。因为不是重点内容，这里就不多赘述啦。）

现在再让我们来做道题！

练习

Suppose a mobile phone company wants to determine the current percentage of customers ages 50+ who use text messaging on their cell phones. How many customers ages 50+ should the company survey in order to be 90 percent confident that the estimated (sample) proportion is within 3 percentage points of the true population proportion of customers ages 50+ who use text messaging on their cell phones? Assume that p′ =0.5.

解析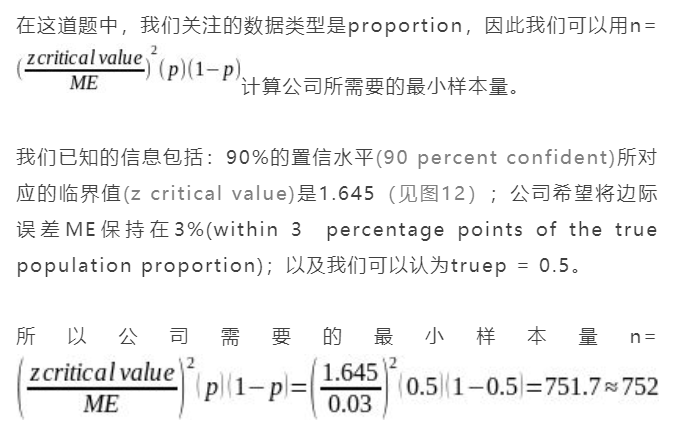

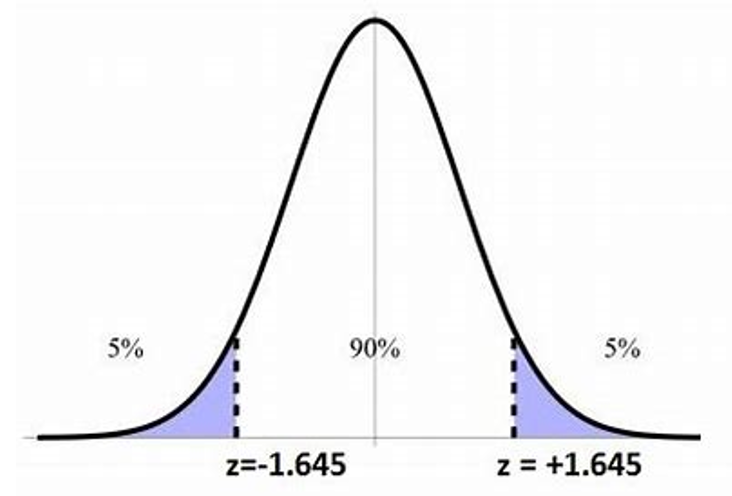
图12

【易错点】

算出来的最小样本量n如果是一个小数，我们要把这个小数近似成比它大的最小整数。比如7517≈752,36.1≈37,20.45≈21，而不是四舍五入噢！因为我们希望在资源允许的情况下获取尽可能大的样本量，以让我们做出准确的预测。

【Tips提示⚠️】其实大家不用特意去记计算最小样本量的公式的！因为它可以由置信区间中的边际误差ME=(critical value)(standard deviation) 推出来！

结 语

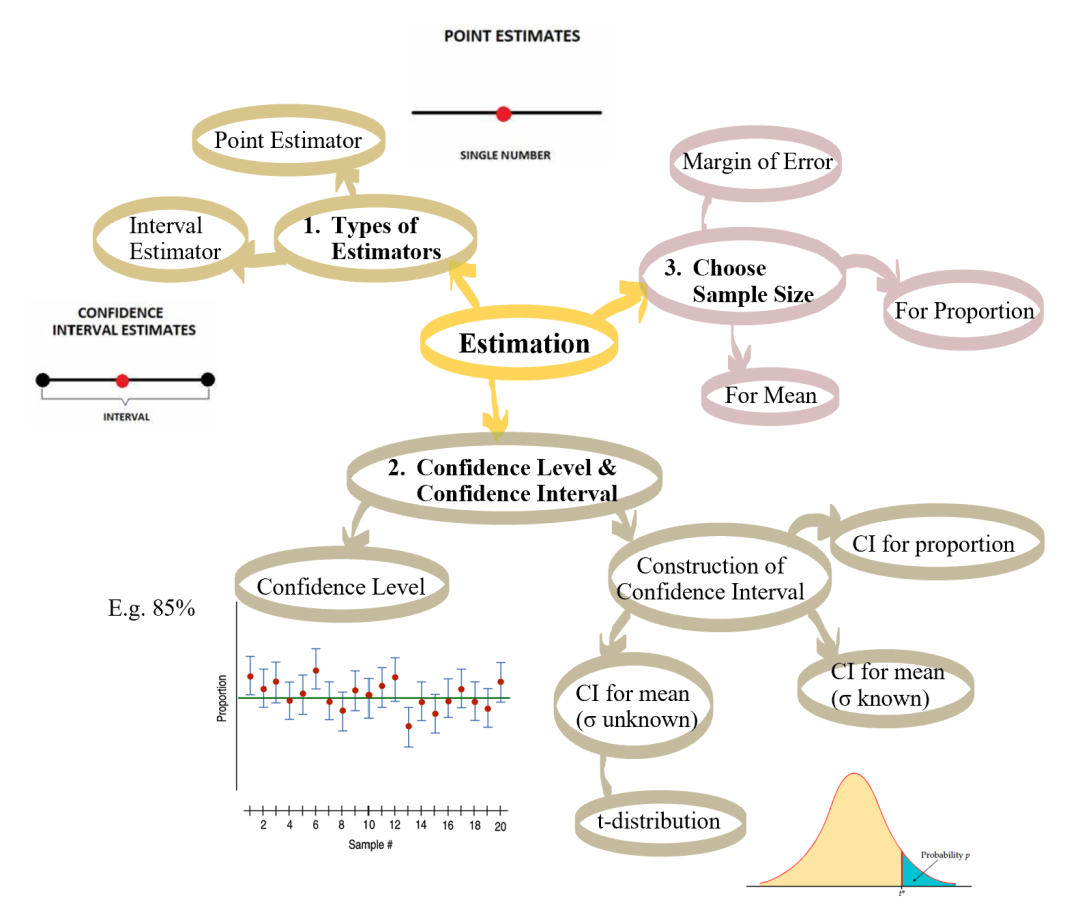
希望这期推送能帮助你掌握estimation这种统计推断方法，学会通过构造置信区间预测总体参数所在的大致范围。

老师为大家总结了下面利用下面这张思维导图，快来来check一下你的掌握程度吧！