AP预备微积分整体考情来啦!
由于预备微积分今年第一次考,没有往年真题,因此备考时College board的AP classroom和College board的sample test是复习首选材料。学生的考试反馈也印证了这一点。
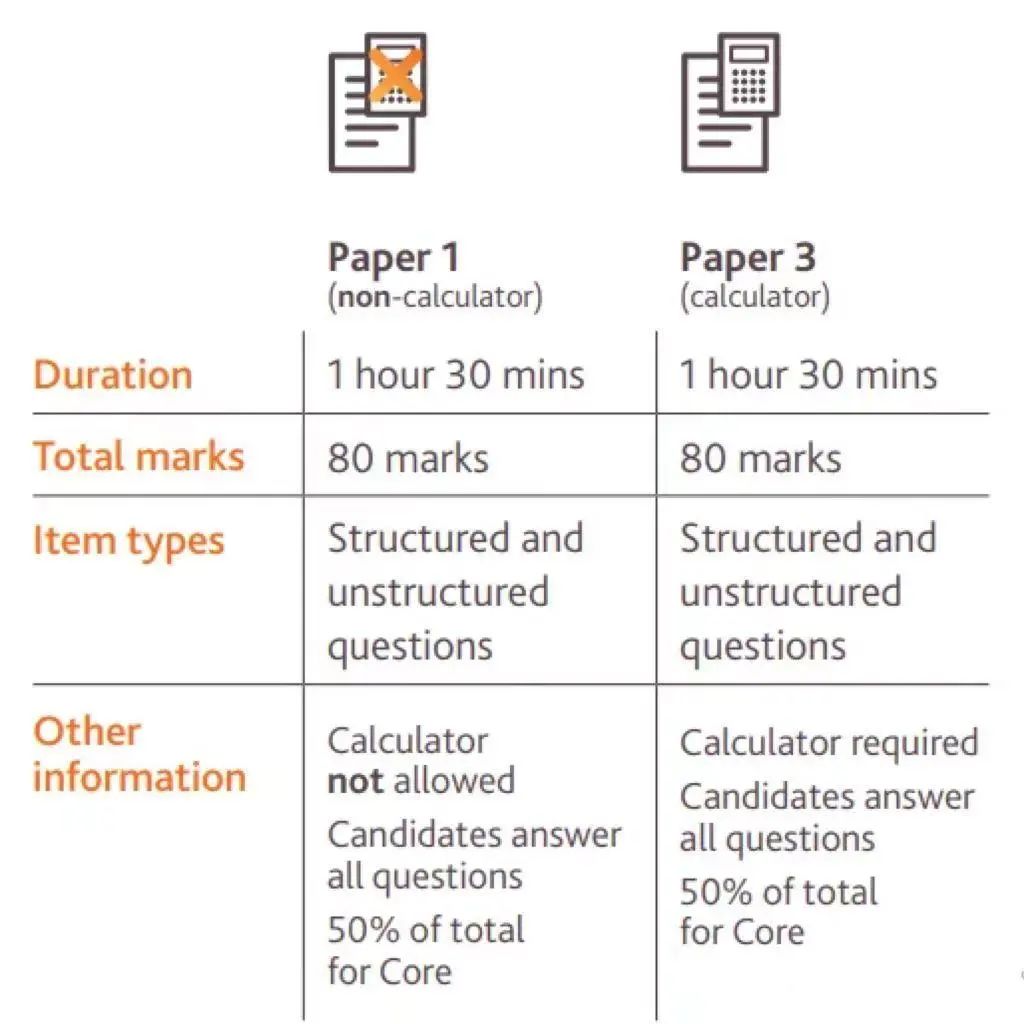
考试中计算器的使用尤为重要,回归、画图等计算器的各种操作必须很熟悉,有些题目不用计算器会得出错误答案。因此如何使用图形计算器是预备微积分的教学中必须要重视的部分。老师邀请到国际课程数理组的李老师为大家带来详细解析!
同学反馈:考前老师为大家总结过的重难点,这次都考到了!!
2024AP预备微积分考情解析
MCQ
总体来说,预备微积分的知识点不多,这场的考试难度适中,基本就是AP classroom 里的题型。
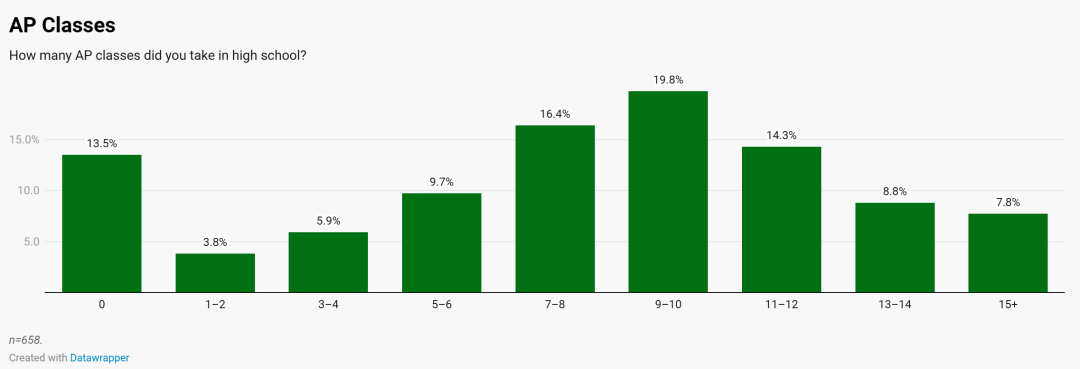
⭐️选择题考点的占比分布如下,难点在Unit 3 Trigonometric and Polar Functions。

FRQ整体考情
据同学反馈,这次AP考试FRQ出的和AP classroom和官Sample test的大题套路是一致的。考点集中且比较少,因此复习起来也比较简单。
FRQ大题解析
大题一(可以用计算器)

✅A问的解析
1)考察复合函数的运算,用计算器求指数函数的值。
✔️复合函数运算:先算里层函数再算外层函数。H(3)=g(f(3)) 先算f(3)=1 再算g(1)
✔️计算器求指数函数值:算g(1)的值。这个很简单,直接计算即可。
2)考察直角坐标图像的识别,在图像上画一条平行于x轴的直线:y=1。(这条直线上所有点的纵坐标都是1)(不是平行于y轴的直线,教学中有同学会搞混),然后看直线与函数交点的横坐标。
✅B问的解析
1)考察计算器使用,用计算器解出g(x)=2的解。如果是使用TI-Nspire CX CAS计算器的同学可以用”solve函数”求解。
2)考察指数函数性质。极限符号。
这道题可以用计算器画图,但是比较慢。最快的方法是,老师讲过y=ab^x 这个标准指数函数的性质,这道题中0
✅C问的解析
考察一个函数有没有反函数及其原因,这个知识点是重点知识点,一个函数如果不是0ne-to-one function(不能通过horizontal line test:随便给平面直角坐标系画与x轴平行的直线,只要有一条与图像交于2个及2个以上点,就不通过horizontal line test),那么这个函数就没有反函数。很显然,f(x)没有反函数。
大题二(可以用计算器)

✅A问的解析
1)考察题意的理解:要知道G(t)和t的意义,然后把t=0时g=40以及 t=91时g=76代入即可。
2)考察用计算机求解方程组,解出a和b即可。如果是使用TI-Nspire CX CAS计算器的同学在菜单里选择解方程组即可。
✅B问的解析
1)考察Average rate of change(平均变化率):平均变化率只和始末点有关,文中能看出始末点为(0,40)(91,76),用平均变化率公式(y2-y1)/(x2-x1)计算即可。
2)考察点斜式(point-slope form)本题实际上考察过始末两点(0,40)(91,76)的直线的方程。
第一问求出了直线方程斜率(平均变化率),第二问带入两个点中任一一个点即可。比如带入(0,40),用点斜式(point-slope form)(y-40)/(x-0)=斜率,可以轻松求出直线方程。再将t=50带入,就能算出估计的G(t)值
3)考察图像凹凸性(concavity),这个性质在AP calculus AB/BC(微积分)中也有考察。
因为此函数为ln函数, 并且b>0(递增),因此呈现concave down(凸)的趋势,直线在ln函数的下方。因此,估计值小于函数值。
✅C问的解析
函数的拟合范围。关于拟合问题的大题,拟合范围基本上是必考的,出题人想告诉学生拟合函数只能在一个范围内适用,不能不加范围限制。
本题中的t不管取任何数,对数函数模型G(t)是递增的,但t>91时,真实的卖游戏的数量在递减,这是与模型不符的。
大题三(不能用计算器)
三角函数终于来啦,这道题和之前AP classroom以及sample test的题神似。


✅AB问的解析
周期(period)=5/2-1/2=2直接得出b=2Π/2=Π最大值18 最小值0直接得出a=(18-0)/2=9 d=(18+0)/2=9根据题意,T=1/2时h=0,可画出A问的五个点。最后将任意点坐标带入函数表达式求出c即可。
✅C问的解析
1)考点
✔️正负性:函数的纵坐标都大于零,函数为正positive
✔️增减性:函数是增函数还是减函数。
2)考点:
✔️凹凸性:函数是“凹的”还是“凸的”
大题四(不能用计算器)


✅A问的解析
1)指数函数与对数函数:利用指数函数与对数函数互为反函数的规律,以及对数函数的定义,求解函数。
反三角函数:把反三角函数化成正常的三角函数,再利用特殊角求解函数。
2)对数性质:利用对数的power rule, product rule以及quotient rule把几个对数合并(condense)
三角性质:把所有的三角函数全部化为sin和cos,再进行运算。并且考查:sin^2(x)+cos^2(x)=1
3)考察三角函数和反三角函数的复合函数:先把反三角函数化成正常的三角函数,求出tan(2x)的值,然后再利用tan函数的图像及周期性求出所有x。
以上就是今年的考情解析,预备微积分真的非常“新手友好”,即使基础薄弱也可以学。