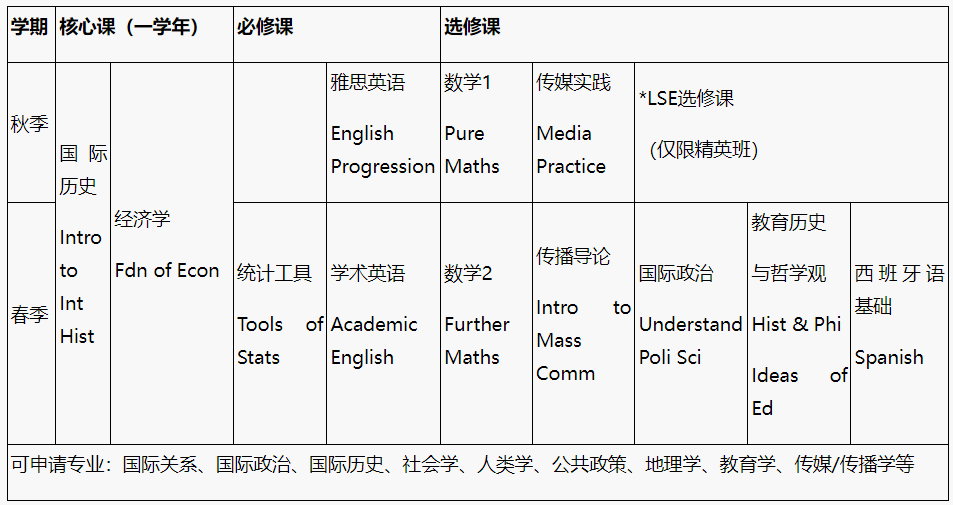
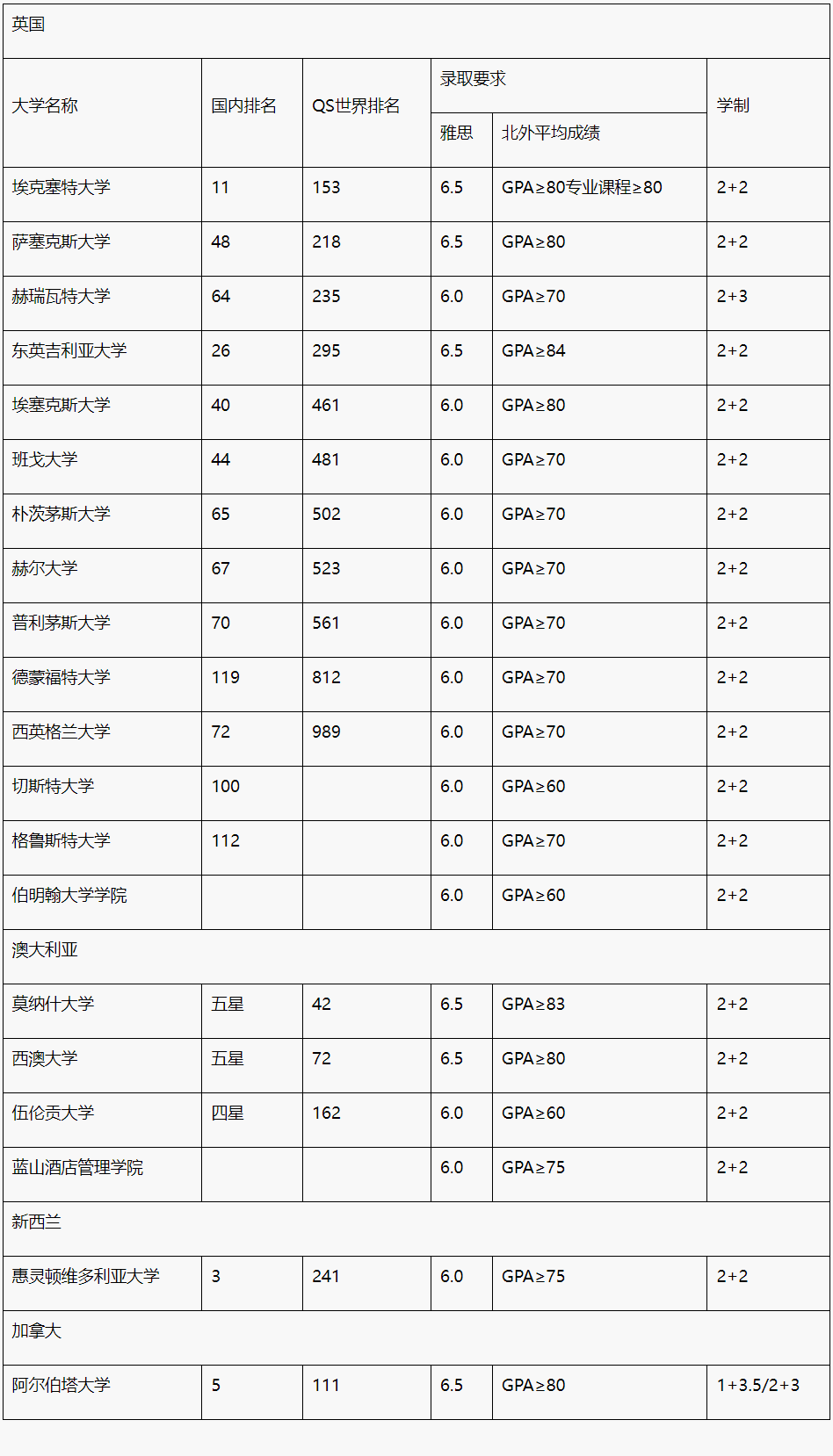
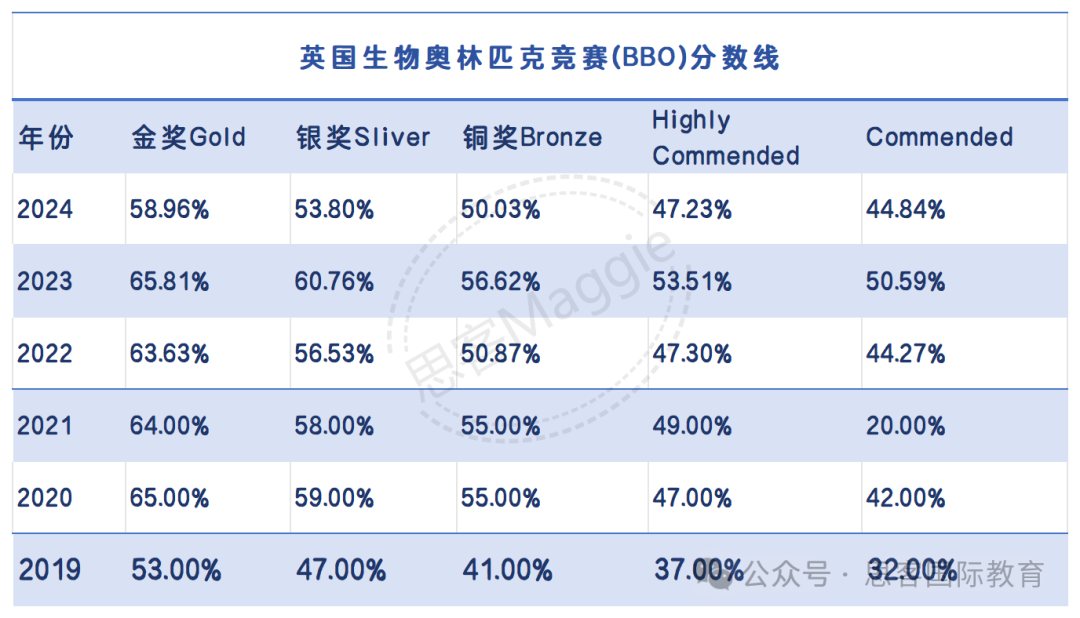
2024AP大考已迫在眉睫,特别邀请到老师为同学们圈画AP微积分AB/BC考试重点和答题要点!AP 微积分大部分的题目都是非常有逻辑的数学计算,选择题会以结果为导向,而大题有不少需要同学们把过程展示出来。
今天给大家明确几个可以去重点复习的大题题型,会分成有计算器和无计算器两部分给大家分别提醒。
*注:对微积分BC同学适用,微积分AB同学可以自行过滤后参考。
计算器大题注意事项
写在最前面:务必保证计算器是radian模式(不能是degree),此外进考场可以准备两个计算器,建议一个可以画图,一个负则计算。

有计算器的大题分成两类:
1. 参数方程
2. 文字题
参数方程&运动学大题目注意事项:
1、distance与displacement务必观察区分到位,二者公式绝对不能记错,distance只需要积分一次,但是displacement需要分水平位移以及垂直位移,需要积分两次,一定要观察清楚方向,speed与velocity也要区分,speed只是一个数值,没有正负反向,但是velocity会有水平速度以及垂直速度,可以写成向量形式(一般题目给的条件都是速度向量,注意区分
2、加速度的向量写法,计算器部分肯定会对计算器的操作有一定要求,历年都会出现加速度的向量计算考察,需要仔细计算,最后写成向量的写法(求导不能忘记链式法则)
3、运动学结合参数方程会考察切线方程的书写,参数方程求解一阶导的时候公式不能记错,尤其是会出现一些比较临界的情况(比如水平切线注意是dy/dt=0并且dx/dt≠0;垂直切线是dx/dt=0并且dy/dt≠0,不要忘记检验)
参考2006以及2023FRQ


文字题大题注意事项:
1、 注意结合应用题的时候都会结合单位进行描述,单位要看清是求导之后还是积分之后单位,不能看错
2、 注意变化量与总量的区别,尤其是总量很多同学会在最后一步忘记加初始数值,这点绝对不能忘记,积分的运算有解析式就交给计算器,如果是利曼和就分清利曼种类和区间跨度,
3、 求最值的时候不要忘记算出local之后需要结合左右端点进行共同列表比较大小,如果出现分段函数的处理不要忘记观察区间进行分步积分
参考2007以及2017FRQ


大家可以快速过一下这两个题目,关注一下题目的问法,尽量手动按一下计算器。
非计算器大题注意事项
非计算器大题部分,分为三个板块:
1. 微分方程2. Taylor3. 计算技巧
微分方程注意事项:
1、 注意切线方程预估的计算,一定要求出切点所在的一阶导数作为切线方程斜率(斜率可以根据题目的dy/dx代入点进行计算)
2、判断切线与原函数位置关系注意是观察原函数的开口方向(即二阶导的正负),原函数开口向上,切线在原函数下方,属于underestimate,反之则是overestimate
3、可分离微分方程解题必须要按照分步进行踩分,首先必须变量分离再进行各自积分,常数必须积分完毕之后马上跟上,然后就是代入初始点算出常数,最后整理得出解析式

级数/泰勒展开考点:
1、 注意泰勒系数与每一阶导数之间的关系来进行判断local max/min的操作(主要是一阶导与二阶导的符号处理计算)
2、 泰勒展开当中的拉格朗日error bound计算处理公式要注意加强,尤其是可能会出现和图片结合的模式,可以参考一下2011年出现的大题

积分技巧大题目:
1、 首先关注洛必达的计算(现在几乎每年大题目必有洛必达的极限计算),注意洛必达使用的前提条件必须书写到位,再进行分子分母的各自求导
2、 大题目如果出现by parts,一定要把u 和dv变量设置到位,分步的计算要写清楚,尤其是dv设置的时候不要忘记最后需要把dx也写进去
3、Improper 计算的时候不要忘记书写格式,出现无穷的地方需要用一个字母的极限进行替换,有时候也会出现结合洛必达共同处理进行计算
4、IVT与MVT的使用条件以及使用范围要注意,IVT只需要保证连续性即可,求出的范围是不需要对原函数进行求导的(连续性的证明不要忘记左右极限以及本身取值的三者相等),MVT不要忘记闭区间的连续以及开区间每一个点可导(开区间条件最容易忽略corner是连续但不可导的),算出来的结果也是需要结合一阶导进行计算的,所以审题时候要看仔细是否有导数出现在题目里
5、利曼和的预估要分清左利曼还是右利曼还是梯形利曼,此外每一段区间的跨度不一定是等长的,也需要看清要求不能主观盲目
6、 最后是积分求导的组合考点,这是每年必考内容,注意积分求导三步口诀