美国大学理事会举办的AP考试的微积分科目,分为微积分AB和微积分BC,这两门课注重学生对微积分概念的理解,并提供方法和应用经验。
微积分这门学科从极限入手,引出微积分的重要概念、定义、公式和定理以及各类重要应用。这是一门强调推理论证、方法技巧以及应用的学科。
AP考纲解读
Calculus
AP微积分AB/BC区别与选择
学习AP微积分之前,需要有一定的数学基础,比如代数、几何、三角学、解析几何和初等函数等 ,这些函数包括线性函数、多项式、有理函数、指数函数、对数函数、三角函数、反三角函数和分段定义函数,并掌握函数的性质、运算法则和图像。还必须理解函数的语言(域和范围、奇数和偶数、周期、对称、零、截距以及诸如递增和递减之类的描述符)。
另外,也需要知道知道如何从单位圆定义正弦和余弦函数,以及在0、π/6、π/4、π/3、π/2及其倍数处的三角函数值。
出分率对比
AP微积分BC的内容全覆盖微积分AB内容,难度也更大,它相当于大学第一学期和第二学期的微积分课程。两门课有百分之六七十的重合度,但其实每年AP微积分BC的5分率都大大高于AP微积分AB的5分率。AB每年的5分率约在19%,BC每年的5分率约在40%。
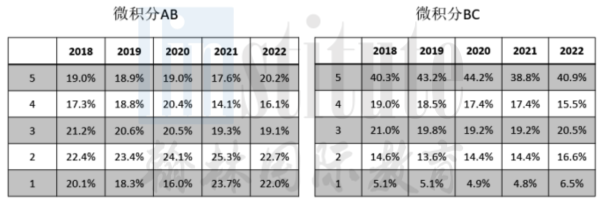
另外AP微积分BC在大学的认可度和能够转换学分的概率都更高。参加微积分BC的考试之后,可以拿到两个分数,一个是BC的,一个适合AB的。微积分BC拿到满分5分的情况下,也会获赠微积分AB的满分成绩,这就是常常出现的微积分双5分的情况。
AP微积分5分率这么高的一个原因是:AP微积分的容错率非常高。满分108分的卷子只需要拿到70分左右就可以拿到5分,基本是三分之二的正确率即可。
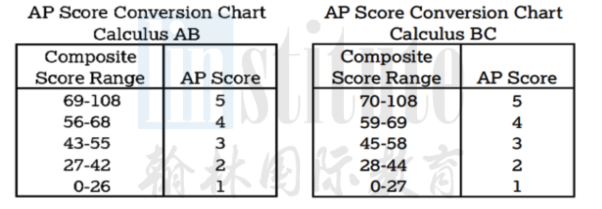
知识点对比
下面我们来看看AP微积分AB与BC的考点分布:
● 第1单元:极限与连续性
● 第2单元:微分:定义和基本属性
● 第3单元:微分:复合函数、隐函数和反函数
● 第4-5单元:微分的各类应用
● 第6单元:积分
● 第7单元:微分方程
● 第8单元:积分应用
● 第9单元:参数方程、极坐标和向量方程
● 第10单元:无穷序列和级数
AP微积分AB与BC的主要区别在第九单元和第十单元,这两个章节是BC only的,包括参数方程,极坐标系,向量方程,以及无穷级数部分。
其他章节的内容覆盖也有部分区别:
● 第3-5单元微分以及应用部分,多了极坐标方程,参数方程求导,在motion中多了二维运动,求切线中增加了polar形式的切线求解;
● 第6单元积分部分,BC会包含分部积分法,分式拆分法以及瑕积分;
● 第7单元微分方程部分,BC会包含欧拉公式,以及logistic模型;
● 第8单元积分应用部分,BC会包含弧长积分,曲线路径积分,增加参数形式的定积分和二维运动等。
下图是选择题的单元知识点分布表:
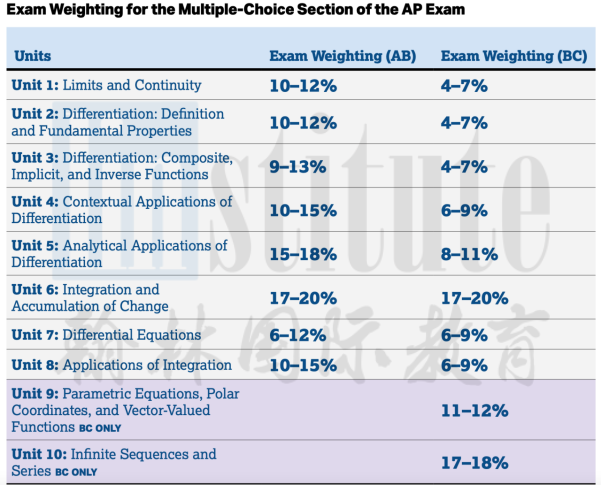
可以看到第九单元和第十单元占了BC的30%左右,而这最后两个章节,尤其无穷级数是重难点部分。其实选择BC只比AB多了一小部分内容。
然而由于学习BC在大学的认可度和能够转换学分的概率都更高,所以学习BC很有优势。当然做出选择还要参考未来的专业选择。
未来专业对AB/BC选择的影响
选择微积分BC的情况
● 未来想申请数学、计算机、生物、化学、科学、普通商科及管理类甚至是医学等相关专业
● 对于未来专业选择生物化学、社会科学、普通商科及管理类的同学而言,BC基本涵盖了大学本科所有的教学内容,拿到5分并兑换AP学分,意味着大学不需要再修习微积分课程。
● 对于专业方向是数学、计算机、物理、工程或经济、金融等专业的同学,BC能相当好的满足后续学习要求。
选择微积分AB的情况
● 未来想申请社会或人文等学科专业
● 想要更弹性的时间安排,为其他的学科学习预留足够的时间
Calculus
AP微积分考试形式与重难点
了解课程的整体框架,清楚每部分的重点内容,有目标性地进行学习,更能把AP微积分学懂、学好,5分到手更有把握!
AP微积分允许部分使用计算器:
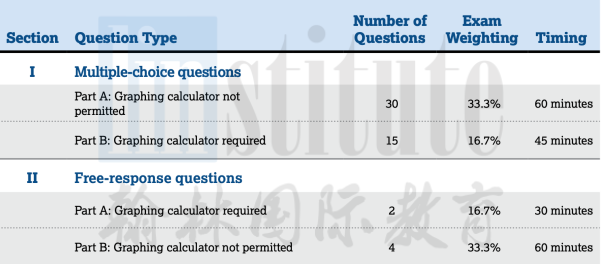
✏考试时长:3小时15分钟
✏考试形式:45道多项选择题和6个自由回答问题。
● 第一部分:多项选择题,45题,105分钟,占考试成绩的50%
A部分:30个问题;60分钟(不允许使用图形计算器;占33.3%)
B部分:15个问题;45分钟(需要图形计算器;占16.7%)
● 第二部分:自由回答,6题,90分钟,占考试成绩的50%
A部分:2个问题;30分钟(需要图形计算器;占16.7%)
B部分:4个问题;60分钟(不允许使用图形计算器;占33.3%)
AP微积分的这十个章节中,我们可以从前文的章节考试百分比看出考试的重点分布,以BC为例,重点在于求导应用、积分以及积分应用、无穷级数这些部分。
而难点部分以及需要注意的部分有:
极限部分
需要注意的是,我们不仅要熟练掌握洛必达法则,用洛必达法则处理无穷大比无穷大,或者零比零的分式极限,还需要掌握如何处理零乘无穷大,零的无穷大次方,无穷大的零次方类似问题的处理方式。另外注意掌握求导定义的含义,有的极限题目需要我们透彻了解求导定义之后方能解答。
求导应用部分
注意微分中值定理罗尔定理等定理的应用,以及相关题目的处理方式。
积分部分
注意曲线积分,二维运动的路径长度求解,极坐标面积积分,运动物理总运动路程求解,旋转体体积积分,注意体积积分时候绕x轴、y轴旋转的不同处理方式等。还要注意积分中值定理的应用。
微分方程部分
注意掌握斜率场含义和图像,欧拉方法以及logistic增长曲线的形状等。
无穷级数部分
这个重难点,注意区分p级数、调和级数、几何级数以及交替级数;注意通用的级数发散的判别方法,注意对于正级数的几种敛散性的判别方法的选用,注意它们之间的区别。比如积分判别法,比较判别法,极限比较判别法,比值判别法,n次根式判别法,这些判别法各自的适用条件,如何选用以及如何用它们判断敛散性。另外交替级数有它特殊的判别方法也需要多加区分注意。
考试中对于选择题和简答题,考察不同能力的占比如下表:


选择题中,Practice 1 也就是考察从数学公式到运算结果的部分占整个考试的53%到66%的比重。包括 differentiation 以及 integration 的计算以及对应的应用,例如算体积、面积、rate of change 等等。而定理的直接考察或证明或验证等的考察占比较小。平时学透彻,结合多刷真题,刷分类的知识点的选择题,会很有助于提分。
做大题时候不仅仅要写出答案,还要能够解释以及使用专业术语,并且把过程中的表达式写出来,如果仅仅写个答案,可能只拿1分,很多问题需要我们去解释说明清楚,才能拿高分。
Calculus
AP微积分的备考建议
在进入微积分学习之前需要有较好的函数基础,AP微积分学习五大类初等函数的微积分,所以对于幂函数,指数函数,对数函数,三角函数,反三角函数的性质,图像,公式定理,求解方法需要很熟悉,反函数,复合函数等也是需要提前掌握。Pre-calculus就是进入AP微积分前的一个很好的铺垫。
在理解的基础上再学习技巧
学习数学需要技巧和理解,二者缺一不可。理解原理与AP微积分需要我们深入理解原理,理解求导定义式,理解各定理的原理以及思想,有一些题目是直接考察我们对于原理的掌握。重视公式推导,推导是最好的记忆方法,推导之后理解也更加透彻,运用也更加熟练。在这个基础上需要分类学习各个版块的知识点,方法技巧,掌握各类题型的解题方法技巧,比如掌握不同的积分表达式应该选用什么积分方法,不同的无穷级数应该选用什么判别敛散性的方法,等等。
常回顾,常梳理归纳总结,常复习
知识点常常是环环相扣的,前面的内容为后面的铺垫和基础,学习过程中常复习可以为后续学习做好铺垫,常梳理归纳总结可以找到同一个知识点不同题型之间的区别与联系,找到处理不同类型题目的不同的方法技巧,掌握如何选用最有效的方法进行求解。
整理错题集
错题集是很有必要的,而且需要常回顾,因为比如积分方法中,原式变换一点点可能就需要使用完全不同的积分方法来求解,初学容易遗忘或出错,那么整理错题集可以帮助我们快速复习回顾,加深之前出错点的正确解法的印象,加上常复习,可以渐渐达到融会贯通的效果。
考前刷真题套卷
之前是分模块地刷每个部分的知识点,考前需要大量刷真题套卷,一方面把握好时间分配,模拟考场感受,一方面整体的复习回顾各个部分的知识点,了解试卷整体知识点分布,查缺补漏自己的薄弱知识块,并进行针对性的复习。最后几套当做全真模考来做,严格计时。
熟练使用计算器
考试中会有约33%的部分需要使用计算器,需要能够熟练掌握计算器的使用方法,平时就要做好练习,了解每种情况下的计算器使用方法。
计算器的选用中,比较好用的是Ti-Nspire和Ti-84这两种。
不论是哪款计算器,请确保会进行以下四个操作:
● 能用计算器画函数图像,并且熟练地缩小和放大窗口;
● 能用计算器找函数的零点(zero point),即解方程;
● 能用计算器计算函数在某一点的导数(derivative);
● 能用计算器计算定积分(definite integral)
另外,考试中有67%的部分不能使用计算器,所以平时要做好计算训练,考试时间紧,题目多,需要手算的地方也不少,所以计算能力强可以得到准确结果以及节省做题时间,这些平时都要做好训练。
遇到难题卡住时间较长时进行取舍判断,随时关注时间。
注意备考时间
如果是学校学习,3月一般会学完所有知识点,一个月时间刷题;如果是社会考生,一般需要30-50(如果没有多少precalculus基础需要的学习时间较长)小时的上课时间以及大量的练习,最后也要有至少一个多月的时间刷真题套卷复习巩固比较好。
最后希望大家放松心态,认真练习,在考试中取得好成绩,在学习中有所收获。