AP物理1关于Momentum动量的知识点详细解析

在本期推送中，我将带着大家一起来了解AP物理1中有关动量（Momentum）的知识。

首先，什么是动量呢？

 尽管物理学中的momentum常常被翻译成“动量”, 但我们知道日常语言中的momentum还可以表达“势头”、“动力”、“冲力”等含义（比如我们可以说“We gained momentum to study AP Physics.”我们超级有动力去学习AP物理），会发现和物理中的momentum的含义是很贴近的。 

所以我们可以将momentum理解为物体继续向前方运动的趋势（就像我们努力不停歇地学习AP物理一样），而这一趋势的大小与物体的质量(mass)和速度(velocity)有关。 接下来，就让我给大家讲解一下AP物理中momentum相关的重要知识点。

文章目录

1 Momentum and Impulse 动量与冲量

2 Representations of Changes in Momentum 动量变化的表示

3 Open and Closed Systems: Momentum 开放系统与封闭系统

4 Conservation of Linear Momentum 动量守恒

5 Collision 碰撞

6 Tips：易错知识点&补充

Momentum and Impulse动量与冲量

(A) Momentum 动量

正如上文所提到的，一个物体的动量指的是这个物体在它运动方向上保持运动的趋势，它等于物体的质量和它运动速度的乘积，也就是下面这个耳熟能详的公式：

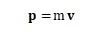
这个公式其实很符合我们的直觉：质量大、移动速度快的物体（比如在高速公路上飞奔的大货车）的运动状态不容易被改变，也就是它保持其原运动状态的趋势会更大； 相比之下，质量小、移动速度慢的物体（比如缓慢滚动的皮球）的运动状态会更容易被改变，也就是它保持原运动状态的趋向会更小。 

通过观察这个公式，我们会发现动量p=标量m × 矢量v，我们可以推断出动量是一个矢量(vector），因此它的大小与方向都需要被考虑进去。而m（也就是质量）是没有方向的，所以物体的动量(p)的方向一定与其运动速度(v)的方向（也就是运动的方向）相同。 

千言万语总结成一句话：一定要记住动量(momentum)是矢量矢量矢量，计算的时候一定要考虑方向方向方向！！以及对应好速度的正反方向和正负号，非常重要！

而大家所熟知的牛顿第二定律(Second Law of Motion)就是用动量来表达的：施加在一个物体上的合外力=单位时间内物体动量的变化，也就是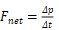（虽然我们更熟悉的牛顿第二定律的表达是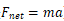）。不过不要被它俩的外表所迷惑！ 如果我们进行仔细观察和对比，就会发现它们本质上是一样的（在物体的质量不变的情况下）：

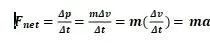
(B) Impulse 冲量
接下去我们来讲下冲量这个概念：如果我们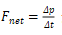将进行小小的转化，我们将得到动量的另一个表达式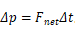：。我们给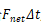赋予一个新名字：冲量(impulse)，它等同于动量的变化。
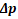如果我们把动量的变化视为外力对物体的作用效果，会发现这个作用效果既取决于力的大小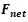，也取决于它作用在物体上的时间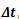。也就是说，一个很小的力也可以引起很大的动量变化，只要它的作用时间足够长。 听上去是不是有点抽象，我就这给大家举个例子：

假设你的小伙伴和你打赌谁敢从高台跳到地板上（大家不要轻易模仿！），你既不想认输，但又十分珍爱生命，这时候，掌握关于冲量的知识或许能帮助你。  

我们知道，如果人体内的骨头受到太大的力，就会骨折。也就是说，当你从高台跳到平地上时，如果你的双腿在一瞬间直接落在坚硬的地面上，地面对你施力的时间极短，你的腿受到的力和冲击是巨大的（想想就觉得很疼有木有！）。 

但如果你跳下来后选择在地上滚来滚去，或者选择作弊用降落伞着陆，都可以延长(地面对你的腿施加的)力的作用时间，在同样的impulse下，你的腿受到的力就会大大减小。（尽管这样你骨折的概率会小很多，但为了你的身心健康，还是建议尽早和这个小伙伴绝交hh。）

Representations of Changesin Momentum动量变化的表示

前面的第一部分我们的讨论都是围绕单个物体展开的，但是如果我们将前文中的“物体”替换成“系统”，结论依然是成立的。

 对于一个质量不变的系统（系统内的每个物体质量不变)而言，这个系统的动量的变化=系统里每个物体的质量之和与这个系统质量中心（center of mass）*的速度变化之积： 

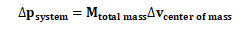
*AP Physics 1 只考察对于center of mass概念的理解，不要求对其进行计算 

同时，一个系统动量的变化也=施加在系统上的平均力（average force）与力施加的时间之积，即施加在系统上的冲量：

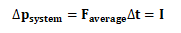
这个关系也可以在图像中表示。如果用图像表示力-时间，它可能长这样： 

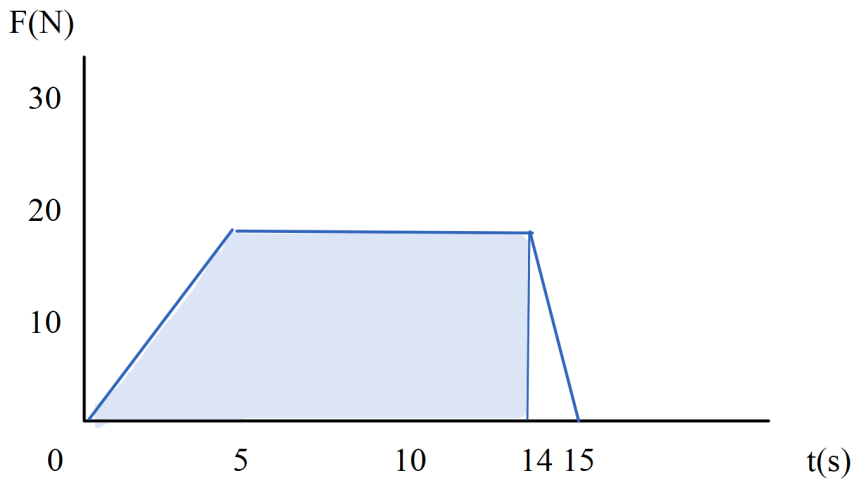
在这一图象中，0-14s之间curve与横轴之间的面积=0s-14s之间施加在系统或一个物体上的冲量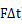（），也=0s-14s中此系统或物体动量的变化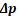（）。 还记得v-t图像中curve与横轴之间的面积=物体的位移x吗？动量和位移的变化在图像上的表示是十分类似的。 如果题目在提供图像的基础上，还告诉了我们m或v任意一个变量，我们就可以通过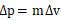很容易地求出另一个未知量。 

Open and Closed Systems

Momentum 开放系统与封闭系统

在了解动量守恒之前，我们需要先一起来区分open system（开放系统）和closed system（封闭系统）这两个概念。这里的系统指的是一个物体或者是几个物体的集合，这里的物体一般被默认没有内在的结构。（I.e. The objects are treated as having no internal structure.） 简单来说，开放系统（open system）受到外力做功，系统内的物体可以与系统之外的环境交换能量、动量；而封闭系统（isolated system/closed system）不受任何外力的影响，只有系统之内的物体相互作用的内力，系统能量、动量保持恒定。 

需要注意的是，系统与其环境之间的界限是人为界定的，为了简化情况或方便分析，系统的界定有可能发生改变。 让我们来假设这样一个情况：一个小球从空中往下落。 

如果我们把小球自身看作一个系统，这就是一个open system，因为小球受到重力这个外力（重力是外力是因为重力是由地球向小球施加的，而地球在我们现在界定的系统之外）； 如果我们把小球和地球的集合看作一个系统(ball-Earth system)，忽略空气阻力，那么这是一个closed system，因为没有外力对这个系统做功，小球受到的重力属于系统内部的内力（地球在我们现在界定的系统之内）；但如果在ball-Earth system的基础上，考虑空气阻力，它就变成了open system，因为空气阻力是系统之外的外力。 

Conservation of Linear Momentum 动量守恒
在不受外力的封闭系统中，动量是守恒的（conserved）。由于动量是矢量，当我们说动量保持恒定(momentum remains constant)的时候，动量不仅在大小而且在方向上也要保持恒定。

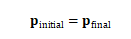
你可能会想说：你说动量守恒它就守恒？凭啥啊？ 

来让我们再一起想象一下：现在有一辆汽车没刹住车，撞向了另一辆汽车。当前面的车(标记为m2)被后面的车(标记为m1)碰撞时，两辆车沿同一方向滑行。如果我们忽略摩擦力，那么每辆车受到的合外力就是对方对自己施加的碰撞的力。由于碰撞，m1受到m2的阻碍速度变小了，失去了一些动量；而m2受到m1的推动速度变大了，获得了一些动量。

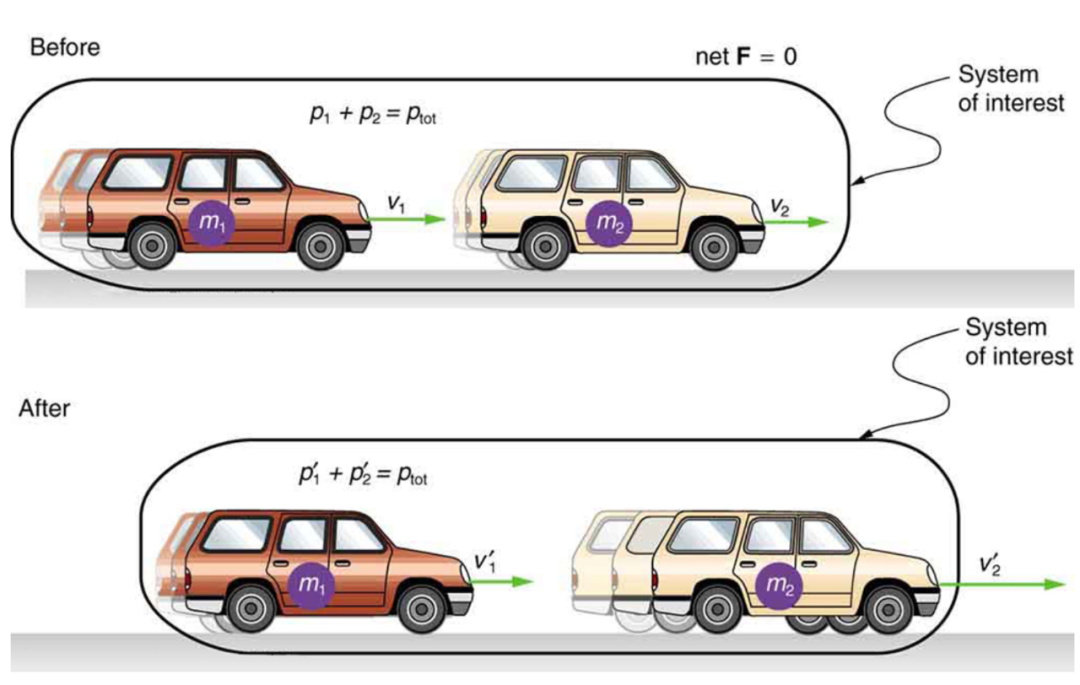
我们知道以下这些量：

1. 根据冲量的定义，第一辆车的动量变化是Δp1 =F1 Δt，第二辆车的动量变化是Δp2 = F2Δt。其中，F1是汽车2对汽车1施加的力，F2则正好相反。

2.两辆汽车的碰撞彼此的持续时间Δt相同。

3.根据牛顿第三定律，F2= -F1。

综上所述，Δp2 = −F1Δt=-Δp1，两辆汽车动量的变化是相等而方向相反的。Δp1 +Δp2 = 0，两辆车的动量的变化量之和为零，这意味着两车构成的系统的总动量是恒定的，即p1+p2 =常数。这两辆车以伟大的奉献精神向我们展示了动量如何在不受外力的封闭系统中守恒。 

Collision 碰撞

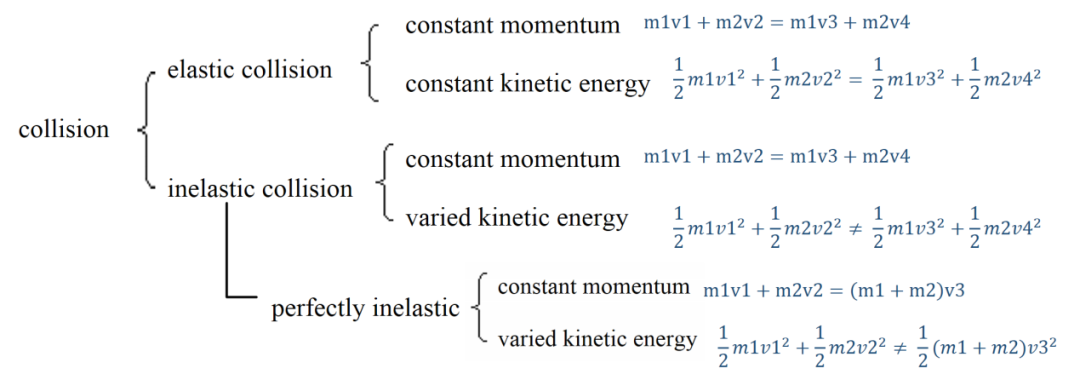
动量与能量守恒常常在两个物体相互碰撞(collision)的情况下考察。我们需要知道两种碰撞类型：弹性碰撞(elastic collision)和非弹性碰撞(inelastic collision)。 Elastic collision 的表现主要为两个物体在碰撞后立即向相反的方向弹开；inelastic collision一般表现为两个物体在碰撞后往一个方向继续运动，其中在完全非弹性碰撞(perfectly inelastic collision)的情况下，两个物体会粘着彼此往一个方向移动

不论是哪种类型的碰撞，由于物体在碰撞的过程中只有物体的相互作用，没有外力施加在这个（只含相互碰撞的两个物体的）系统上，动量(momentum)是守恒的。然而动能(kinetic energy)只在elastic collision中守恒，在inelastic collision中会有损耗。 以下思维导图是一个小小的概括： 

Tips：易错知识点&补充

最后给大家一道判断题来康康你们的掌握程度吧~

判断正误：一个动量(momentum)变化了的物体，其动能(kinetic energy)也一定变化。

答案：错误！

一个动量(momentum)在变化的物体，其动能(kinetic energy)可能保持不变。因为动量是一个矢量(vector)，它可以变化方向而不改变大小（还记得我在第一部分的怒吼吗！），在这种情况下，物体的动能不变。

最后的最后，给大家分享（不太严谨的）冷笑话一则：

我在走廊上散步的时候，总有好朋友恶作剧般猛地冲向我，使我以极快的速度弹出老远，每当这时我都会幽幽地说一句：mv=mv。 

好啦，希望本期的内容对大家AP物理1中动量部分的学习有所帮助~