众所周知,AP物理4门在2024-25学年迎来了重大调整,在考试形式、题型设置、知识点分布上均有不小的改革。
在AP物理C当中,虽说CB官方仅以“考点顺序调整”以描述物理C的考纲变化,但在实际的学习过程中,我们还是会接触到不少新增的知识点。

为大家详细介绍来自Unit 2的新增考点:牛顿壳层定律,干货满满请务必收藏!
#01新增考点:Newton's Shell Theorem
壳层定理是牛顿提出的经典物理理论,它清晰地描述了球对称分布的质量如何产生引力场。
这一定理不仅简化了复杂的引力问题,也为我们理解天体、行星及工程中的球体结构提供了重要工具。
在旧考纲中,我们往往只需要关心天体外部的引力分布,而在新考纲的要求下,我们需要讨论球体内部的引力场分布了。
#02壳层定理的两个关键点
壳层定理主要包括以下两个关键结论:
外部引力场
对于一个球对称分布的物体(无论是实心球还是空心球壳),在球体外部任意一点,整个球体对外部物体的引力作用可以等效为将其所有质量集中于球心产生的效果。
引力强度公式为: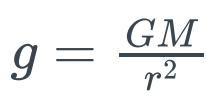
,r>R其中M是球体的总质量,R是球体的半径,r是讨论对象距球心的距离。
壳内部引力场
对于一个球对称的空心球壳(即中间为空的球体),在壳层内任意点,净引力始终为零。这是因为球壳内各部分的质量对该点的引力相互抵消。
空心球壳的内部引力公式:
![]()
#03实心球的引力场分布
外部引力场
在实心球的外部,壳层定理告诉我们,引力强度等效于将整个球体的质量集中于球心:

内部引力场
在实心球的内部,壳层定理还说明,某点的引力场仅由球心到该点以内的质量决定,而该点以外的质量对其引力完全抵消。
内部质量的计算:
假设球的总质量M均匀分布,球心到某点半径r范围内的质量
![]() 为:
为:

引力场公式:
距离球心r的引力强度为:

其中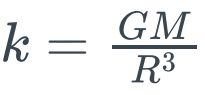
为常数,由此可得在实心球内部的引力场强度与距离r成正比。
引力场的特点:
在球心处 (r=0) ,引力场强度为零;
引力场强度 随距离r成正比线性增加;
随距离r成正比线性增加;
在球表面 (r=R),引力强度达到最大值:
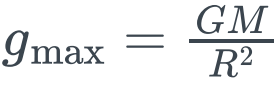
#04空心球壳的引力场分布
外部引力场
空心球壳的外部引力场与实心球一致,即:
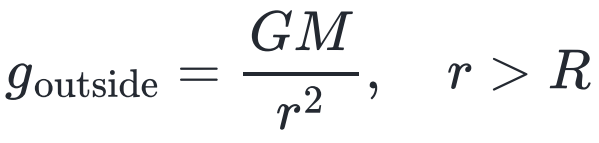
内部引力场
在空心球壳的内部,任意点的引力场均为零:
![]()
原因:这是由于球壳内各部分的质量对壳内物体的引力相互抵消,无论物体在壳内何处,其感受到的引力场都为零。
#05引力场分布曲线
以下是实心球和空心球壳的引力强度g随距离r变化的图像:
实心球
从球心(r=0)到球表面(r=R),引力强度随 线性增加。
在球表面(r=R)达到最大值后,随反r²比减小。
空心球壳
在壳外(r>R),引力强度与实心球一致,随r²反比减小。
在壳内(r<R),引力强度为零。
#06绘制引力场曲线图
接下来为这两种情况绘制g与r的关系曲线。
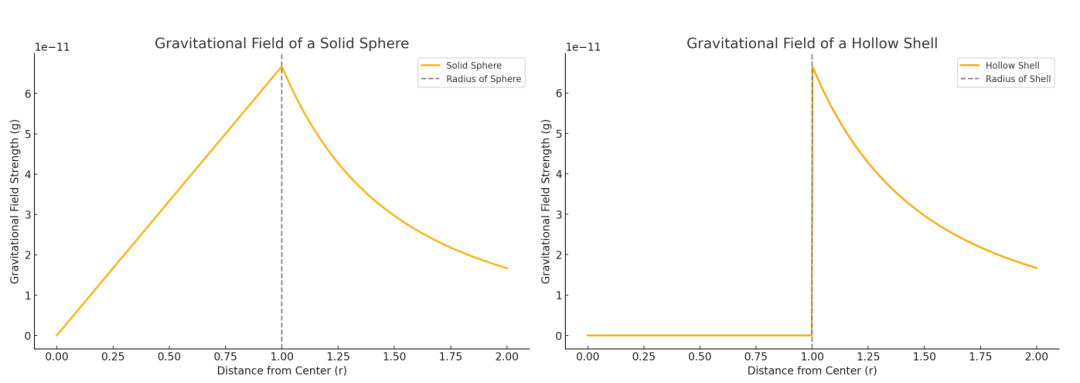
以上是实心球和空心球壳的引力强度g随距离r的变化曲线:
实心球引力场分布
在球体内部(r≤R),引力强度随r线性增加(成正比)。
在球体外部(r>R),引力强度随距离的平方反比减小。
空心球壳引力场分布
在球壳内部 (r<R),引力强度始终为零。
在球壳外部 (r≥R),引力强度与实心球外部一致,随距离的平方反比减小。
这两幅图清晰地展示了壳层定理的关键特性,为理解球对称分布的引力场提供了直观的帮助。
总结:
以上就是AP物理C中有关Shell Theorem的全部内容啦,其本质就在于分清球体内部和外部的引力场分布。
总的来说,在球体内部时,如果物体处于空心部分,则该处的引力场强度g=0,如果处于实心部分,则引力场强度g会随着物体到球心距离r的增加呈线性关系。
在球体外部时,我们就可以单纯将球体本身作为一个整体(当成一个质点考虑),其引力场强度就可以直接利用万有引力定律推导得出g与距离r成平方反比关系。












