今年武外英中AS年级秋季期中考试数学(高数班)P3重点考察了以下几个知识点:代数(绝对值、长除法、分式分解、二项展开)、对数函数、三角函数以及微分。小编听任课老师说,这次考试难度适中,不算特别难~涉及到的题型甚至是原题在我们以赴的复习课上也都有讲过哦。让我们一起看看这次考试的几个重点题型,温故而知新吧!
01、Algebra(Modulus Inequalities)
代数(模数不等式)
【常见题型】
【难度系数】??
【考点分析】该题考察学生含绝对值不等式的解法。
【思路点拨】通过不等号两边同时取平方去掉绝对值符号,转变为一元二次不等式。
【评分标准】

02、Algebra(Division of polynomials)
代数(多项式除法)
【常见题型】Find the quotient and remainder when x4is divided by x2+ 2x -1. [3]
【难度系数】??
【考点分析】该题考察学生多项式之间的除法。
【思路点拨】通过长除法依次得出商和余。
【评分标准】

03、Logarithmic and exponential functions(Logarithmic equations)
对数和指数函数(对数方程式)
【常见题型】Showing all necessary working, solve the equation ln(x4 – 4) = 4lnx – ln4, giving your answer correct to 2 decimal places.[4]
【难度系数】??
【考点分析】该题考察学生是否掌握对数方程的解法,其中ln为底数是自然常数e的对数。
【思路点拨】先根据对数运算法则将等号两边合成单项,再根据对数的单调性对应相等即可。
【评分标准】

04、Further algebra(Partial fractions and binomial expansion)
进阶代数(部分分式与二项式展开)
【常见题型】

【难度系数】????
【考点分析】该题考察了学生对于分式分解与二项展开的掌握情况。
【思路点拨】通过分式分解的规则写出含未知数的分解结果,再通过系数对应相等解出未知数,得到分解结果,然后根据二项展开的相关公式计算即可。
【评分标准】
(i)
State or imply the form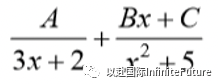 |
B1 |
| Use a relevant method to determine a constant | M1 |
| Obtain one of the values A = 2, B = 1, C = -3 | A1 |
| Obtain a second value | A1 |
| Obtain the third value | A1 |
| Total: | 5 |
(ii)
Use correct method to find the first two terms of the expansion of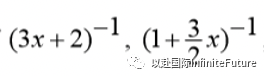 , ,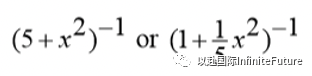 [Symbolic coefficients, e.g. [Symbolic coefficients, e.g.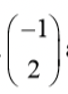 are not sufficient] are not sufficient] |
M1 |
Obtain correct unsimplified expansions up to the term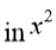 of each partial fraction. The FT is on A, B, C from part (i) of each partial fraction. The FT is on A, B, C from part (i) |
A1FT+A1FT |
Multiply out up to the term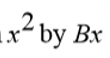 + C, where BC ≠ 0 + C, where BC ≠ 0 |
M1 |
Obtain final answer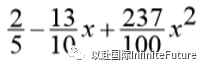 , or equivalent , or equivalent |
A1 |
| Total: | 5 |
05、Trigonometric(Trigonometric identities)
三角函数(三角恒等式)
【常见题型】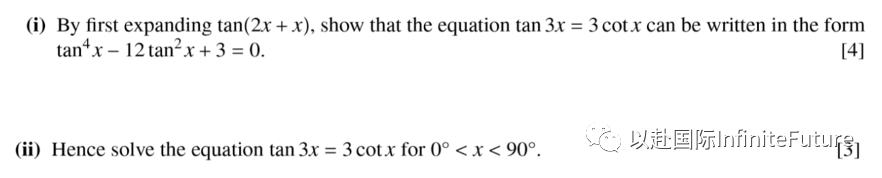
【难度系数】???
【考点分析】该题综合考察不同类型的三角函数以及三角函数的计算。
【思路点拨】根据复合角以及二倍角三角函数的公式,对等式左边进行展开化简,然后将等式右边转换为常见的三种三角函数,继续化简即可。
【评分标准】
(i)
| Use tan(A + B) formula to express the LHS in terms of tan2x and tanx | M1 |
| Using the tan2A formula, express the entire equation in terms of tanx | M1 |
| Obtain a correct equation in tanx in any form | A1 |
| Obtain the given form correctly | A1 |
| Total: | 4 |
(ii)
| Use correct method to solve the given equation for x | M1 |
| Obtain answer, e.g.X = 26.8° | A1 |
| Obtain second answer, e.g.X = 73.7° and no other | A1 |
| Total: | 3 |
06、Trigonometric(Trigonometric identities)
三角函数(三角恒等式)
【常见题型】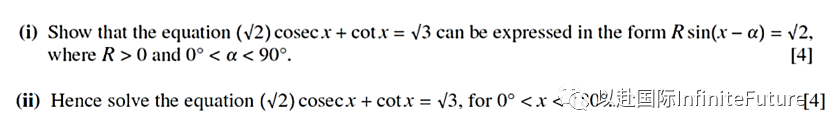
【难度系数】???
【考点分析】该题综合考察不同类型的三角函数以及三角函数的计算。
【思路点拨】先将等式左边出现的三角函数转换为常见的三种类型,然后根据复合角公式写成题目要求的形式,再解出具体的x即可。
【评分标准】
| (i) Rearrange in the form √3sinx - cosx = √2 | B1 |
| State R = 2 | B1 |
| Use trig formulae to obtain α | M1 |
| Obtain α = 30º with no errors seen | A1 |
| Total: | 4 |
(ii) Evaluate |
B1ft |
| Carry out a correct method to find a value of x in the given interval | M1 |
| Obtain answer x = 75º | A1 |
| Obtain a second answer e.g. x = 165º and no others. [Treat answers in radians as misread. Ignore answers outside the given interval.] | A1ft |
| Total: | 4 |
07、Differentiation(Derivatives of trigonometric functions)
微分(三角函数的导数)
【常见题型】
【难度系数】???
【考点分析】该题考察了学生三角函数的导数计算方法。
【思路点拨】根据链式法则以及三角函数求导公式进行求导,再根据三角函数性质以及stationary points的性质即一次导数等于0,求出待证的表达式,解出x。
【评分标准】
| (i) Use product rule Obtain correct derivative in any form | M1 A1 |
| (ii) Equate derivative to zero and use correct cos(A + B) formula Obtain the given equation | M1 A1 |
(iii) Use correct method to solve for x obtain answer, e.g.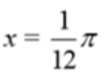 Obtain second answer, e.g. Obtain second answer, e.g.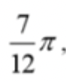 and no other and no other |
M1 A1 A1 |
08、Differentiation(Derivatives of logarithmic functions)
微分(对数函数的导数)
【常见题型】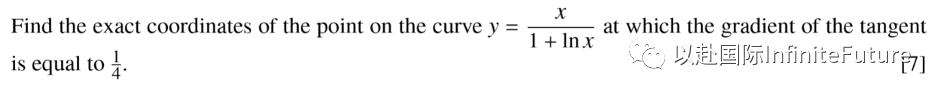
【难度系数】???
【考点分析】该题考察了对数函数的导数计算方法。
【思路点拨】根据除法求导法则以及对数函数求导公式进行计算,再令导函数等于斜率值接触x即可。
【评分标准】
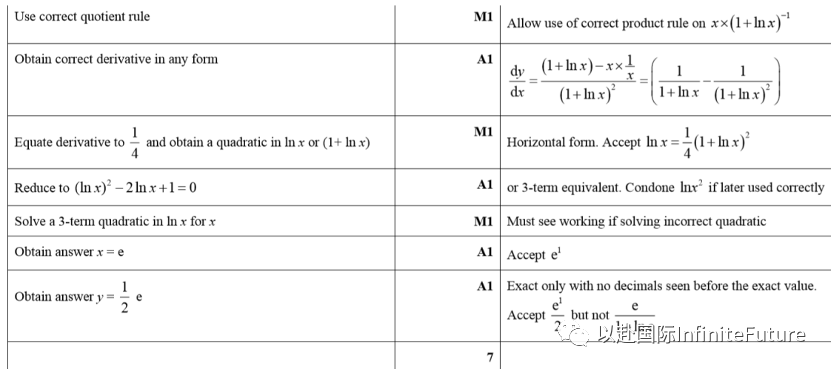
09、Differentiation(Parametric Differentiation)
微分(参数微分法)
【常见题型】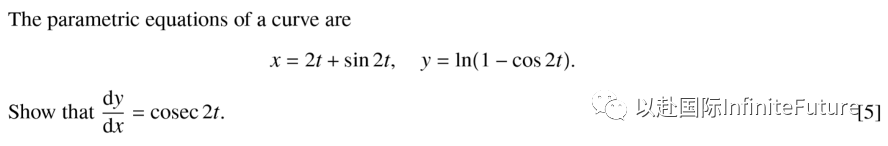
【难度系数】???
【考点分析】该题考察了学生参数方程的导数计算方法。
【思路点拨】分别求出x和y对参数的求导结果,然后相除即可。
【评分标准】

010、Differentiation(Implicit differentiation)
微分(隐微分法)
【常见题型】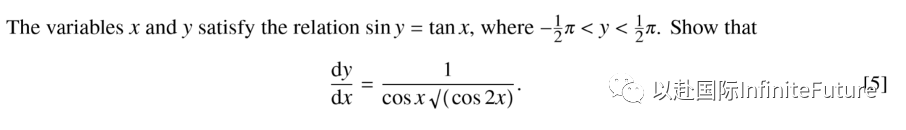
【难度系数】???
【考点分析】该题考察隐函数的导数计算方法以及简单的三角函数求导。
【思路点拨】等式两边的同时对x进行求导,然后将结果分离出来即可。
【评分标准】