A Level进阶数学究竟学什么考什么？

今天就来给大家介绍一下A Level进阶数学（further maths）科目的内容以及这一方面的大学申请，各位学弟学妹们赶紧搬好小板凳拿好小本本我要开讲了。

A Level进阶数学究竟考什么

俗话说“知己知彼，百战百胜”，考试也是同理，如果同学们想要考好A Level进阶数学，那肯定要先了解自己学习和考试的内容。同学们可以在CAIE官网上去找syllabus content，这个部分会告诉你每一单元的考试内容和范围以及分值还有考试时间。

A Level进阶数学一共要考4张paper（4场考试），分别是further pure mathematics 1（FP1），further pure mathematics 2（FP2），further mechanics（FM）还有further probability&statistics（FS）

FP1

Paper1的考试内容主要分为多项式的方程根，有理函数和图形，系列的综合，向量，极坐标，矩阵以及归纳证明。这一张paper的学习以及考试内容将会是学paper2以及paper3内容的基石。所以即使觉得简单的同学们还是要严肃对待。考试时长一共两个小时。

 FP2

Paper2的考试内容包含双曲函数，矩阵，微积分，复数以及微分方程，虽然paper2的考试内容和paper1相比会少一点，但是考试时长也是两个小时。

 FM

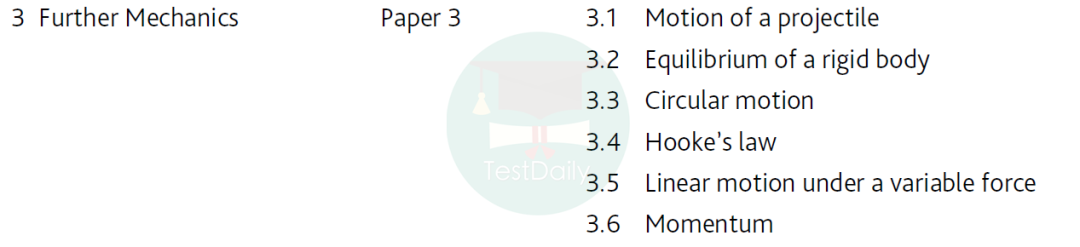
Paper3的考试内容包含动能（抛射物），刚体平衡，圆周运动，胡克定律，变力作用下的直线运动以及动量。这一张paper的学习内容对于学A Level物理的小伙伴们来说就比较简单啦（因为大多数都和物理重复了），paper3的考试时间为一个半小时。

 FS

Paper4的考试内容看标题就知道是围绕着可能性和统计学考试的，主要内容是连续随机变量，使用正态分布以及t分布进行推理，非参数检验以及概率生成函数。（个人肤浅地认为是AS进阶版统计学）考试时间为一个半小时。

Assessment objectives（AO）

Assessment objective同学们可以理解为是考试局希望从考生的卷子上看到什么/评分标准。A Level进阶数学与数学的AO是一样的，主要分为两部分。

AO1包括在考试中体现出对相关数学概念，技术以及符号的理解和准确回忆并使用适当的数学操作技术；在题目中，AO2则是分为三个点：

1.识别给定情况的适当数学程序；

2.在解决问题时应用适当的数学技能和技巧组合；

3.以合乎逻辑的方式呈现相关数学工作，并传达相应的结果和结论。

Assessment objectives对于A Level的各项科目都是非常重要的，同学们平常的学习也要围绕着这方面去思考。

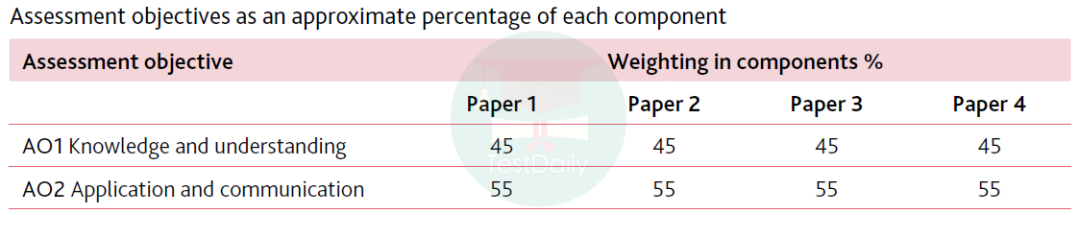
下图是A Level further maths四张paper AO1和AO2的占比（其实基本都一样），进阶数学会更侧重于对于知识点的应用（不然怎么会称之为进阶数学呢hhhh）。

A*/A率以及大学申请

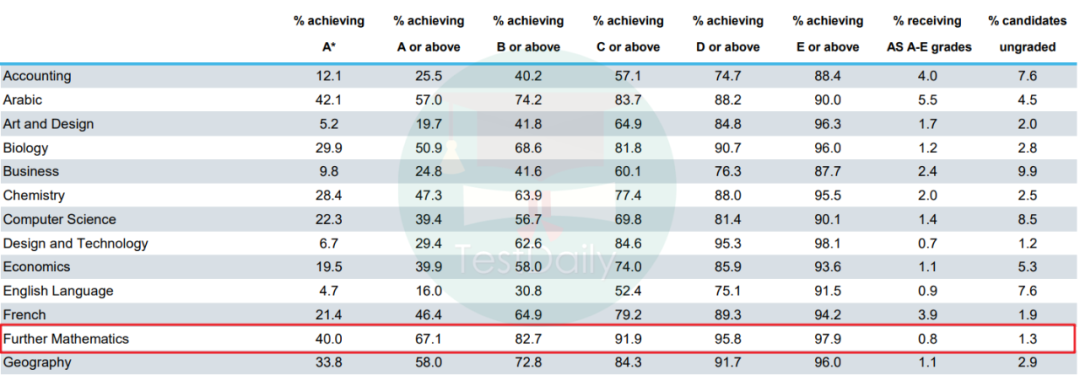
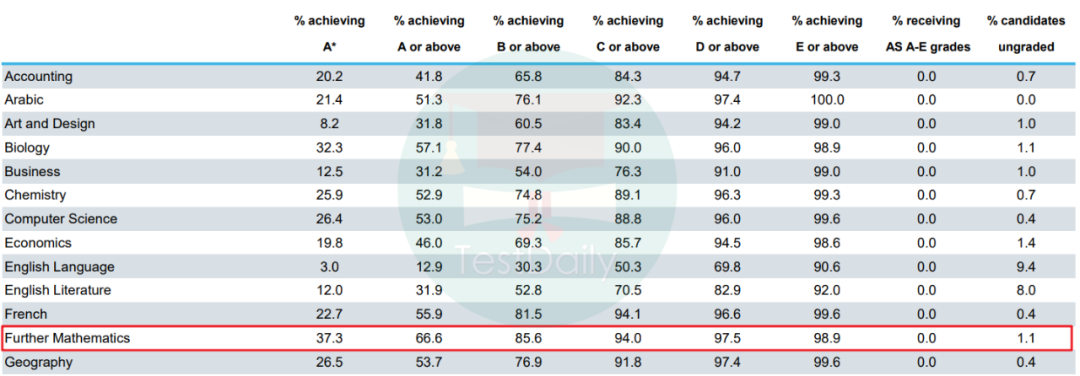
下图分别是来自于CIE官网的2021以及2020年的进阶数学A*/A的数据，2021年的A*率达到40%，2020年也达到了37%。虽然说是官网上的数据，但是客观来看其实还是过于偏高了，据老师当时的英高老师说正常在真正考试的情况下A*可能10%都不到，毕竟进阶数学还是有一定难度的。

推测是因为这两年疫情影响学校老师给的预估成绩都是偏高，但是在英国地区2022年还是正常的线下纸笔考试，所以这方面同学们可以留意一下今年的数据了。

（CIE官网2021年进阶数学A*率）

（CIE官网2020年进阶数学A*率）

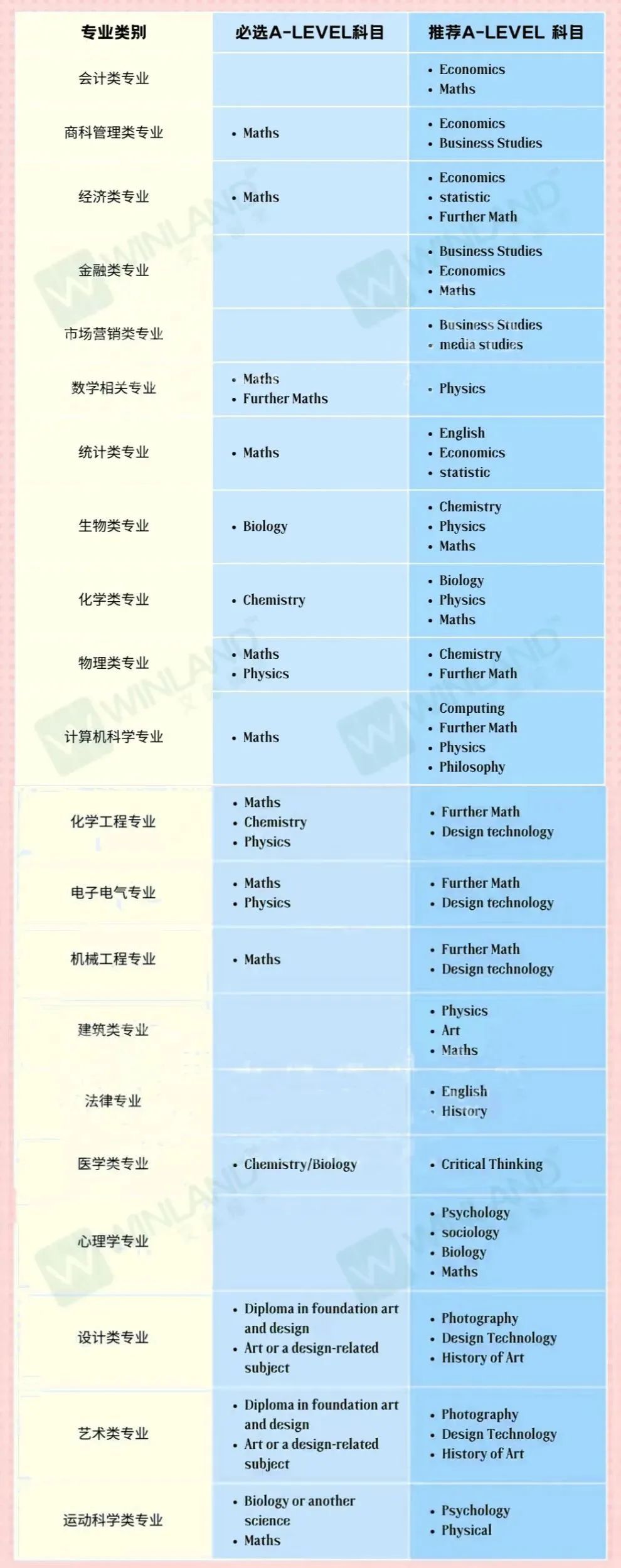
一般来说，如果大学想学纯数，物理或者是经济学的同学们，或者想申请英国G5院校甚至华威的同学们，是一定要学A Level数学以及进阶数学并参加考试（拿A或者A*）的。因为大学给的conditions里面会要求数学和进阶数学同时拿A或者A*（取决于每个学校的专业要求）。

比如说帝国理工的物理专业还有纯数专业，剑桥大学的经济学专业或者LSE的PPE专业等等，不同大学不同专业的要求都是不一样的，（甚至有的大学给不同学生同一个专业的conditional offer上面的conditions都会不太一样）。这一方面同学们具体可以去大学的官网找entry requirement或者往年录取生的成绩统计数据来作为一个参考。

一些学A Level进阶数学需要具备的能力

老师结合了一下CIE的官网信息以及自己学习A Level进阶数学的书从而发现了一些学习和备考进阶数学的必备技能：

解决问题

数学从根本上说是解决问题并以不同的方式表示系统和模型。这些包括：

代数：这是支持和表达数学推理的重要工具，并提供了一种在多种情况下进行概括的方法。

几何技术：代数表示还描述了空间关系，这为我们提供了一种理解情况的新方法。

微积分：这是描述动态情况变化并强调函数和图形之间联系的基本要素。

机械模型：这些模型解释了预测粒子和物体在力的影响下如何移动或保持稳定。

统计方法：这些方法用于量化和模拟我们周围世界的各个方面。概率论预测偶然事件可能如何进行，以及关于偶然性的假设是否有证据证明。

沟通

数学证明和推理使用代数和符号表示，以便其他人可以遵循每条推理并确认其完整性和准确性。数学符号是通用的。每个解决方案都是结构化的，但证明和解决问题也需要创造性和原创性的思考。

数学建模

数学建模可以应用于许多不同的情况和问题，从而产生预测和解决方案。创建模型可能需要各种数学内容领域和技术。创建并应用模型后，可以解释结果以提供有关现实世界的预测和信息。

以上就是关于A Level进阶数学科目学习和考试的一些基本内容以及考试情况，希望能帮助到想学习A Level进阶数学的同学们啦！（虽然有难度但是真的入股不亏~）